
【题目】“三等分任意角”是数学史上一个著名问题,经过无数人探索,现在已经确信,仅用圆规直尺是不可能做出的.在探索过程中,我们发现,可以利用一些特殊的图形,把一个任意角三等分.如图:在∠MAN的边上任取一点B,过点B作BC⊥AN于点C,并作BC的垂线BF,连接AF,E是AF上一点,当AB=BE=EF时,有∠FAN=![]() ∠MAN,请你证明.
∠MAN,请你证明.

科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
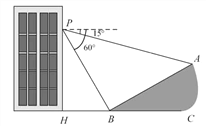
【题目】如图,小明在大楼45米高(即PH=45米,且PH⊥HC)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的
坡度i(即tan∠ABC)为1: ![]() .(点P、H、B、C、A在同一个平面上
.(点P、H、B、C、A在同一个平面上
点H、B、C在同一条直线上)
(1)∠PBA的度数等于________度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用![]() 的材料.
的材料.
(1)求制作每个甲种边框、乙种边框各用多少米材料?
(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数﹣2,B点表示数6,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过 秒,甲、乙两小球到原点的距离相等.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com