
���⣺��֪����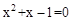 ����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
�⣺�����̵ĸ�Ϊy����y=2x������
�� ������֪���̣���
������֪���̣���
���ã�
������Ϊ
�������÷��̸��Ĵ������·��̵ķ��������dz�Ϊ���������������Ķ������ṩ�ġ������������·��̣�Ҫ�����̻���һ����ʽ��
��1����֪����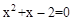 ����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����������Ϊ��
����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����������Ϊ��
��
��2����֪����x��һԪ���η��� ���������������ʵ��������һ��һԪ�����̣�ʹ���ĸ��ֱ�����֪���̵ĵ�����
���������������ʵ��������һ��һԪ�����̣�ʹ���ĸ��ֱ�����֪���̵ĵ�����
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1-2c |
| 2 |
| 1-2c |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| m |
| 2 |
| m |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ���� | x1 | x2 | x1+x2 | x1x2 |
| x2-2x=0 | 0 | 2 | 2 |
0 |
| x2+3x-4=0 | -4 | 1 | -3 |
-4 |
| x2-5x+6=0 | 2 | 3 | 5 |
6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
|
|
|
|
| ||
|
| ||
|
| ��+�� | ||
|
| -3 |
| 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| �� �� | x1 | x2 | x1+x2 | x1•x2 |
| ��1�� | ||||
| ��2�� | ||||
| ��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com