
 完成下面的证明(在括号中填写推理理由)
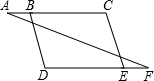
完成下面的证明(在括号中填写推理理由)分析 根据平行线的判定得出AC∥DF,根据平行线的性质得出∠C+∠CED=180°,求出∠D+∠CDE=180°,根据平行线的判定得出即可.
解答 证明:∵∠A=∠F,
∴AC∥DF(内错角相等,两直线平行),
∴∠C+∠CED=180°(两直线平行,同旁内角互补).
∵∠C=∠D,
∴∠D+∠CDE=180°(等量代换),
∴BD∥CE(同旁内角互补,两直线平行),
故答案为:内错角相等,两直线平行,CED,两直线平行,同旁内角互补,CED,等量代换,同旁内角互补,两直线平行.
点评 本题考查了平行线的性质和判定,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 如果一件事发生的机会只有千万分之一,那么它就是不可能事件 | |
| B. | 如果一件事发生的机会达99.999%,那么它就是必然事件 | |
| C. | 如果一件事不是不可能事件,那么它就是必然事件 | |
| D. | 如果一件事不是必然事件,那么它就是不可能事件或随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
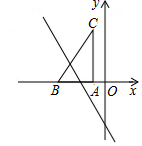 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度.
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(-1,0),(-4,0),将△ABC沿x轴向左平移,当点C落在直线y=-2x-6上时,则点C沿x轴向左平移了4个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com