
【题目】已知:线段MN=a.
![]()
(1)求作:边长为![]() a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
a的正三角形ABC.(要求:尺规作图,不写作法但保留作图痕迹)
(2)若a=10cm.求(1)中正三角形ABC的内切圆的半径.
【答案】(1)作图见解析;(2)(1)中正三角形ABC的内切圆的半径为5cm.
【解析】
(1)作以2a为斜边,∠CBN=30°的Rt△BCN,一条直角边BC为![]() a,以B、C为边作等边三角形即可;(2)分别作CD⊥AB、BE⊥AC于点D、E,CD和BE相交于点O,根据等边三角形的性质可得点O为△ABC内切圆的圆心,OD为半径,BD=
a,以B、C为边作等边三角形即可;(2)分别作CD⊥AB、BE⊥AC于点D、E,CD和BE相交于点O,根据等边三角形的性质可得点O为△ABC内切圆的圆心,OD为半径,BD=![]() AB,利用勾股定理可求出CD的长,设OD=x,在Rt△BOD中,利用勾股定理求出OD的长即可得答案.
AB,利用勾股定理可求出CD的长,设OD=x,在Rt△BOD中,利用勾股定理求出OD的长即可得答案.
(1)作射线BH,在BH上顺次截取BM、MN,使BM=MN=a,分别以M、N为圆心,a为半径画弧,两弧交于点C,连接BC,分别以B、C为圆心,BC长为半径画弧,两弧交于点A,连接BA、CA,△ABC即为所求作的正三角形.

(2)如图:分别作CD⊥AB、BE⊥AC于点D、E,CD和BE相交于点O,
∵△ABC是等边三角形,
∴AD、BE分别是∠ABC和∠ACB的角平分线,
∴点O即为正三角形ABC的内切圆的圆心,OD即为内切圆的半径.
∵a=10,
∴AB=BC=10![]() ,
,
∴BD=![]() AB=5
AB=5![]() ,
,
∴CD=![]() =
=![]() =15,
=15,
设OD=x,
∵OD=OE,
∴OB=OC=15﹣x,
在Rt△BOD中,根据勾股定理,得
OB2=OD2+BD2即(15﹣x)2=x2+(5![]() )2,
)2,
解得x=5.
答:(1)中正三角形ABC的内切圆的半径为5cm.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,若∠DHO=20°,则∠ADC的度数是( )

A. 120°B. 130°C. 140°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连结CD,将线段CD绕点C按逆时针方向旋转90°得到线段CE,连结BE.

(1)求证:△ACD≌△BCE;
(2)当∠1=25°时,求∠E的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则图中阴影部分面积( )

A.![]() π﹣
π﹣![]() B.
B.![]() π﹣5C.2π﹣5D.3π﹣2
π﹣5C.2π﹣5D.3π﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,BC∥AD,∠B=90°,AD边落在平面直角坐标系的x轴上,且点A(5,0)、C(0,3)、AD=2.点P从点E(﹣5,0)出发,沿x轴向点A以每秒1个单位长度的速度运动,到达点A时停止运动.运动时间为t秒.

(1)∠BCD的度数为______°.
(2)当t=_____时,△PCD为等腰三角形.
(3)如图2,以点P为圆心,PC为半径作⊙P.
①求当t为何值时,⊙P与四边形ABCD的一边(或边所在的直线)相切.
②当t______时,⊙P与四边形ABCD的交点有两个;当t_____时,⊙P与四边形ABCD的交点有三个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于点
的图象相交于点![]() 、点
、点![]() ,在
,在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的周长最小,则点
的周长最小,则点![]() 的坐标是____________________________。
的坐标是____________________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)
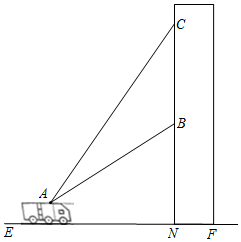
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是![]() 的直径,C是
的直径,C是![]() 上一点,连接AC,过点C作直线
上一点,连接AC,过点C作直线![]() 于D(
于D(![]() ),点E是DB上任意一点(点D、B除外),直线CE交
),点E是DB上任意一点(点D、B除外),直线CE交![]() 于点F.连接AF与直线CD交于点G.
于点F.连接AF与直线CD交于点G.

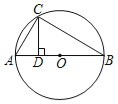
(1)求证:![]()
(2)若点E是AD(点A除外)上任意一点,上述结论是否仍然成立?若成立,请画出图形并给予证明;若不成立,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com