
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF…….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
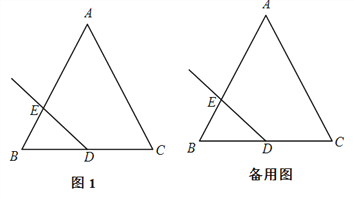
【答案】(1)将图1补全见解析;
(2)证明见解析;
(3)数量关系:当点F在AC边上时, ![]() ;
;
当点F在AC延长线上时, ![]() .
.
【解析】试题分析:(1)根据要求画出图形即可;(2)选择一种自己比较熟练的方法进行证明即可;(3)本题分点F在AC边上,点F在AC延长线上,两种情况分析即可.
试题解析:解:(1)如图1,

(2)
想法1证明:如图2,过D作DG∥AB,交AC于G,
∵点D是BC边的中点,
∴DG=![]() AB.
AB.
∴△CDG是等边三角形.
∴∠EDB+∠EDG=120°.
∵∠FDG+∠EDG=120°,
∴∠EDB =∠FDG.
∵BD=DG,∠B=∠FGD=60°,
∴△BDE≌△GDF.
∴DE=DF.
想法2证明:如图3,连接AD,
∵点D是BC边的中点,
∴AD是△ABC的对称轴.
作点E关于线段AD的对称点P,点P在边AC上,
∴△ADE≌△ADP.
∴DE=DP,∠AED=∠APD.
∵∠BAC+∠EDF=180°,
∴∠AED+∠AFD=180°.
∵∠APD+∠DPF=180°,
∴∠AFD=∠DPF.
∴DP=DF.
∴DE=DF.
想法3证明:如图4,连接AD,过D作DM⊥AB于M,DN⊥AB于N,
∵点D是BC边的中点,
∴AD平分∠BAC.
∵DM⊥AB于M,DN⊥AB于N,
∴DM=DN.
∵∠A=60°,
∴∠MDE+∠EDN=120°.
∵∠FDN+∠EDN=120°,
∴∠MDE=∠FDN.
∴Rt△MDE≌Rt△NDF.
∴DE=DF.
(3)当点F在AC边上时, ![]() ;
;
当点F在AC延长线上时, ![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,错误的有( ).
①一组数据的标准差是它的差的平方;②数据8,9,10,11,1l的众数是2;③如果数据 ![]() ,
, ![]() ,…,
,…, ![]() 的平均数为
的平均数为 ![]() ,那么
,那么 ![]() ;④数据0,-1,l,-2,1的中位数是l.
;④数据0,-1,l,-2,1的中位数是l.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价500元,连续两次降价a%后售价为200元,下列所列方程正确的是( )
A.500(1+a%)2=200
B.500(1-a%)2=200
C.500(1-2a%)=200
D.500(1-a2%)=200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙丙丁四支足球队在全国甲级联赛中进球数分别为:9,9,x , 7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )
A.10
B.9
C.8
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把方程x(x+2)=5(x-2)化成一般式,则a、b、c的值分别是( )
A.1、-3、10
B.1、7、-10
C.1、-5、12
D.1、3、2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中不正确的是( )
A. 平方为9的数是+3或﹣3 B. 立方为27的数是3或﹣3
C. 绝对值为3的数是3或﹣3 D. 倒数等于原数的数是1或﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com