
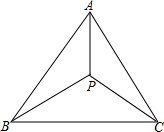
 如图,在△ABC中,AB=AC,点P是△ABC内一点,且∠APB=∠APC.求证:PB=PC.
如图,在△ABC中,AB=AC,点P是△ABC内一点,且∠APB=∠APC.求证:PB=PC. 分析 如图作AM⊥CO交CP的延长线于M,AN⊥BP交BP的延长线于N.由Rt△APM≌Rt△APN,推出PM=PN,由Rt△ABN≌Rt△ACM,推出BN=CM,可得PB=PC.
解答 证明:如图作AM⊥CO交CP的延长线于M,AN⊥BP交BP的延长线于N.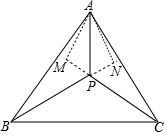
∵∠APB=∠APC,
∴∠APM=∠APN,
∵AM⊥PM,AN⊥PN,
∴AM=AN,
在Rt△△APM和Rt△APN中,
$\left\{\begin{array}{l}{AP=AP}\\{AM=AN}\end{array}\right.$,
∴Rt△APM≌Rt△APN,
∴PM=PN,
在Rt△ABN和Rt△ACM中,
$\left\{\begin{array}{l}{AB=AC}\\{AN=AM}\end{array}\right.$,
∴Rt△ABN≌Rt△ACM,
∴BN=CM,∵PN=PM,
∴PB=PC.
点评 本题考查全等三角形的判定和性质,解题的关键是学会添加常用辅助线面构造全等三角形解决问题,属于中考常考题型.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
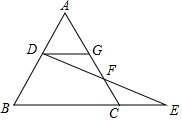 已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.
已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
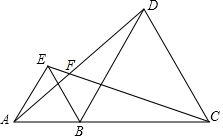 如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).
如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
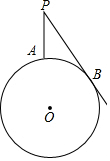 如图,⊙O是地球的轴截面(把地球的轴截面近似地看成圆形),点P表示人造通讯卫星,已知从点P观测到地球表面的最近距离为PA=akm,最远距离为PB=bkm,其中b>a.用a、b表示地球的半径.
如图,⊙O是地球的轴截面(把地球的轴截面近似地看成圆形),点P表示人造通讯卫星,已知从点P观测到地球表面的最近距离为PA=akm,最远距离为PB=bkm,其中b>a.用a、b表示地球的半径.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | ($\sqrt{5}$)2=25 | D. | $\sqrt{16}$=±4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=5}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-4}\\{y=2}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com