
 如图,平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4,那么m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$.
如图,平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4,那么m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$. 分析 易知点P在线段OA的垂直平分线上,那么就能求得△AOP是等边三角形,就能求得点P的横坐标,根据勾股定理可求得点P的纵坐标.把这点代入一次函数解析式即可,同理可得到在第四象限的点.
解答  解:由已知AP=OP,点P在线段OA的垂直平分线PM上.
解:由已知AP=OP,点P在线段OA的垂直平分线PM上.
∴OA=AP=OP=4,
∴△AOP是等边三角形.
如图,当点P在第一象限时,OM=2,OP=4.
在Rt△OPM中,PM=$\sqrt{O{P}^{2}-O{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴P(2,2$\sqrt{3}$).
∵点P在y=-x+m上,
∴m=2+2$\sqrt{3}$.
当点P在第四象限时,根据对称性,P′(2,-2$\sqrt{3}$).
∵点P′在y=-x+m上,
∴m=2-2$\sqrt{3}$.
则m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$.
故答案为:2+2$\sqrt{3}$或2-2$\sqrt{3}$.
点评 此题主要考查了一次函数图象上点的坐标特征,解决本题的关键是求得点P的坐标,需注意点P的两种可能.


科目:初中数学 来源: 题型:解答题
| 类别 | 甲种材料(千克) | 乙种材料(千克) |
| 1件A产品所需材料 | 4 | 1 |
| 1件B产品所需材料 | 3 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
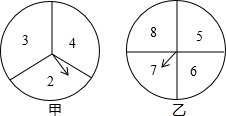 如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
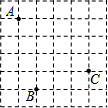 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )| A. | (2,-3) | B. | (1,1) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com