
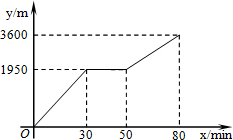
 (2013•德惠市一模)甲和乙上山游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合.已知乙行走到缆车终点的路程是缆车到山顶的线路长的2倍,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min.设乙出发xmin后行走的路程为ym.图中的折线表示乙在整个行走过程中y与x的函数关系.
(2013•德惠市一模)甲和乙上山游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合.已知乙行走到缆车终点的路程是缆车到山顶的线路长的2倍,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min.设乙出发xmin后行走的路程为ym.图中的折线表示乙在整个行走过程中y与x的函数关系.
|
|


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•德惠市一模)学校组织春游,每人车费4元.下面是一班的班长小明与二班的班长小红的对话.
(2013•德惠市一模)学校组织春游,每人车费4元.下面是一班的班长小明与二班的班长小红的对话.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com