
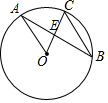
 如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )
如图,已知⊙O的半径为2,点A、B、C为圆上三点,且OA∥BC,则$\frac{1}{CE}-\frac{1}{BC}$的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
分析 根据OA∥BC,得到△BCE∽△NOE,根据相似三角形的性质得到$\frac{OA}{BC}=\frac{OE}{CE}$,代入数据即刻得到结论.
解答 解:∵OA∥BC,
∴△BCE∽△NOE,
∴$\frac{OA}{BC}=\frac{OE}{CE}$,
∵OC=OA=2,
∴OE=2-CE,
∴$\frac{2}{BC}=\frac{2-CE}{CE}$,
∴$\frac{2}{BC}=\frac{2}{CE}-1$,
∴$\frac{1}{CE}-\frac{1}{BC}$=$\frac{1}{2}$,
故选B.
点评 本题考查了相似三角形的判定和性质,圆周角定理,熟练掌握相似三角形的判定和性质是解题的关键,


科目:初中数学 来源: 题型:选择题
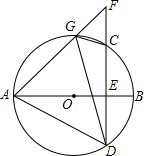 如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )
如图,AB是⊙O直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线相交于点F,连结AD,GD,CG,则与∠AGD相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 工种 | 人数 | 每人每月工资/元 |
| 电工 | 5 | 4000 |
| 木工 | 4 | 3000 |
| 瓦工 | 5 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 平均分 | 中位数 | 众数 | 方差 | 优胜奖率 | 优秀奖率 |
| 初中 | 6.7 | 6 | 6 | 3.41 | 90% | 20% |
| 高中 | 7.1 | 7.5 | 8 | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
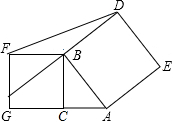 如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.
如图所示,在Rt△ABC中,∠ACB=90°,以AB、BC为边向外作正方形ABDE、BCGF,连接DF,且S正方形ABDE=7,S正方形BCGF=3,则△DBF的面积等于$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪的三个顶点的距离相等,凉亭的位置应选在( )| A. | △ABC三边的垂直平分线的交点 | B. | △ABC的三条中线的交点 | ||
| C. | △ABC三条角平分线的交点 | D. | △ABC三条高所在直线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
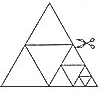 如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )
如图,将一张等边三角形纸片沿任意两边中点的连线可剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,若操作的次数是n时,则可得到的小三角形个数为( )| A. | 3n-1 | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<-4a;④$\frac{1}{3}$<a<$\frac{2}{3}$;⑤b>c.其中正确结论有①③④⑤(填写所有正确结论的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com