
����Ŀ����֪ʶ���ɣ�����֪���������ֲ�ͬ�ķ�������ͬһ������ͼ�ε���������Եõ�һЩ�������ʽ.
���磺��ͼ���Եõ�(a+b)2=a2+2ab+b2�����ڴˣ������������⣺
�� ������ͼ��д��һ���������ʽ��
![]() ��
��
�� ���â��еõ��Ľ��ۣ������������⣺��a+b+c=12��![]() ��
��
��![]() ��
��
�� С��ͬѧ����ͼ��x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ſ������ֱ�Ϊa��b�ij�����ֽƬƴ��һ�����Ϊ(2a+b)(a+3b)�ij����Σ���x��y��z= ��
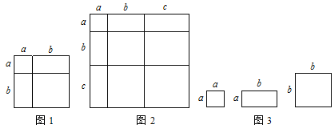
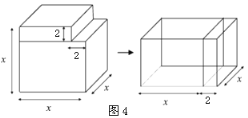
��֪ʶǨ�ƣ��� ���Ƶأ������ֲ�ͬ�ķ������㼸��������ͬ�����Եõ�һЩ�������ʽ����ͼ��ʾ����һ���߳�Ϊx����������ȥһ���߳�Ϊ2��С�����������ƴ��һ���³����壮���������ͼ������ͼ�εı仯��ϵ��д��һ���������ʽ��
���𰸡���(a+b+c)2=a2+b2+c2+2ab+2ac+2bc�� �� 90�� �� 12�� �� x3-4x=x(x-2)(x-2)��
��������
��1�����������ε����=��a+b+c��2�������ε����=a2+b2+c2+2ab+2ac+2bc���ɵõ�ʽ��
��2������a2+b2+c2=��a+b+c��2-2ab-2ac-2bc�����м��㼴�ɣ�
��3��������ƴͼ�ε����Ϊ��xa2+yb2+zab����(2a+b)(a+3b)= 2a2+6ab+3b2�����ɵõ�x��y��z��ֵ��
��4������ԭ����������=�¼�������������ʽ�ɵý��ۣ�
��1����ͼ2�ã������ε����=��a+b+c��2�������ε����=a2+b2+c2+2ab+2ac+2bc��
�ࣨa+b+c��2=a2+b2+c2+2ab+2ac+2bc��
�ʴ�Ϊ����a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��2���ߣ�a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��a+b+c=12��ab+ac+bc=27��
��122=a2+b2+c2+2��27��
��a2+b2+c2=144-54=90��
�ʴ�Ϊ��90��
��3��������ã�(2a+b)(a+3b)=xa2+yb2+zab��
��2a2+7ab+3b2=xa2+yb2+zab��
![]() ,
,
��x+y+z=12��
�ʴ�Ϊ��12��
��4����ԭ����������=x3-2��2x=x3-4x���¼���������=��x+2����x-2��x��
��x3-4x=��x+2����x-2��x��
�ʴ�Ϊ��x3-x=��x+2����x-2��x��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж�Ԫһ�η������Ӧ���⣩ij��˾����3��һ����ģ�Ĵ������2��һ����ģ��С��������������ͬʱ����2���������1��С�������ɹ�300��Ա���Ͳͣ�ͬʱ����1���������1��С�������ɹ�170��Ա���Ͳ�.
(1)����1���������1��С�����ֱ�ɹ�������Ա���Ͳͣ�
(2)���3���������2��С����ȫ�����ţ���ô�ܷ�ȫ��450��Ա���Ͳͣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
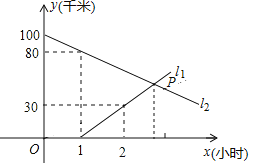
����Ŀ��A��B�������100ǧ�ף��ף��������ﳵ�ֱ��A��B����������У�ͼ��![]() ��
��![]() �ֱ��ʾ���Ǹ��Ե�A�صľ���
�ֱ��ʾ���Ǹ��Ե�A�صľ���![]() ǧ��
ǧ��![]() ��ʱ��
��ʱ��![]() Сʱ
Сʱ![]() �Ĺ�ϵ������ͼ���ṩ����Ϣ������������⣺
�Ĺ�ϵ������ͼ���ṩ����Ϣ������������⣺
![]() ͼ�������߱�ʾ��A�صľ�����ʱ��Ĺ�ϵ��
ͼ�������߱�ʾ��A�صľ�����ʱ��Ĺ�ϵ��
![]() �ף������˵��ٶȷֱ��Ƕ��٣�
�ף������˵��ٶȷֱ��Ƕ��٣�
![]() ��P������꣬������P���ʵ�����壮
��P������꣬������P���ʵ�����壮
![]() �׳����ʱ����������30ǧ�ף�
�׳����ʱ����������30ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ��������ݡ�����һ�վ��У�ѧУ����֧Ϊ���˽ⱾУѧ���ľ������������ȡ��50��ѧ���ľ����������ͳ�ƣ������Ƴ�ͳ��ͼ��
��1����50��ͬѧ��������ΪԪ����λ��ΪԪ��
��2������50��ͬѧ����ƽ������
��3����У����600��ѧ�����������Ƹ�Уѧ���ľ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���߶�![]() ��
��![]() ��
��![]() ��
��
��������ABC��ʹ![]() ��
�� ![]() ��
�� ![]() ��
��

���𰸡��𰸼�����
������������������Ȼ�����![]() ��ȵĽǣ��ٻ���
��ȵĽǣ��ٻ���![]() �ij�������
�ij�������![]() ����
����![]() ������������
������������
�����������ͼ��ʾ�����Ȼ�����BC��
�������Ķ���ΪԲ��,���ⳤΪ�뾶����,�ֱ��������߽���ΪA��,C����
������ͬ����Ϊ�뾶,BΪԲ��,����,��BC�ڵ�F,��FΪԲ��,C��A��Ϊ�뾶���������ڵ�E��
����BF��ȡ��C��ʹCB=a����BΪԲ�ģ�cΪ�뾶��Բ��BE���ӳ����ڵ�A������AC��
���ۣ���ABC��Ϊ����������.

�����͡������
��������
15
����Ŀ����֪���߶�![]() ��
�� ![]() ��������
�������� ![]() ��ʹ
��ʹ![]() ��
�� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����5��д�Ų�ͬ���ֵĿ�Ƭ�����㰴Ҫ������Ƭ��������и����⣺
-3 -5 0 +3 +4
��1������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֵij˻�������˻��� ��
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С����С������ ��
��3������ȡ��4�ſ�Ƭ����ѧ�������㷽����ʹ���Ϊ24��д�������ʽ�ӣ�������д�����֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ABΪ��O��ֱ��AC��ADΪ��O���ң���AB=2AC= ![]() AD�����DBC�Ķ���Ϊ ��
AD�����DBC�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
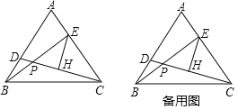
����Ŀ����ͼ���ڵȱ���ABC�У���D����E�ֱ���AB��AC�ϣ�BD=AE������BE��CD���ڵ�P����EH��CD��H��
��1����֤����CAD�ա�BCE����2����֤��PE=2PH����3����PB=PH�����ACD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�������ϵ������㣬��A��ʾ����Ϊ��2����B�ڵ�A�Ҳ࣬����A��12����λ���ȣ�����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮

��1����գ��������ϵ�B��ʾ����Ϊ�� ����
�������ϵ�P��ʾ����Ϊ�� �����ú�t�Ĵ���ʽ��ʾ����
��2����AP��PB���е�ֱ�Ϊ��M��N���ڵ�P���˶������У��߶�M N�ij����Ƿ����仯�����仯����˵�����ɣ������䣬����߶�M N�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com