
分析 问题探究:根据数轴上两点间的距离公式进行计算即可得出两点间的距离;
问题应用:根据(1)(2)中的结论,得出当工作台有奇数个时,工具台应设在最中间一个工作台处,当工作台有偶数个时,工具台应设在最中间两个工作台之间;
问题拓展:根据数轴上两点间的距离公式以及(1)(2)中的结论,求得x在数轴上的位置以及|x-1|+|x-2|的最小值,最后根据以上推理方法可求|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的最小值及x的值.
解答 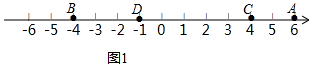 解:问题探究:
解:问题探究:
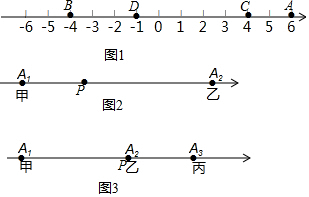
由图1可得,A、C两点间的距离为6-4=2;
B、D两点间的距离为=-1-(-4)=3;
A、B两点间的距离为6-(-4)=10;
E、F两点间的距离可表示为|m-n|;
故答案为:2,3,10,|m-n|;
问题应用:
(3)∵流水线上一次摆着4个工作台A1、A2、A3和A4,为让4名工人拿工具所有的路程和最小,
∴应将工具台设在A2、A3之间的任何地方都行(包括A3和A2);
故答案为:A2、A3之间的任何地方都行(包括A3和A2);
(4)∵流水线上一次摆放着5个工作台A1、A2、A3、A4和A5,为让5名工人拿工具所走的路程和最小,
∴应将工具台设在A3处;
故答案为:A3;
问题拓展:
∵三个点分别为1、2、x,
∴当x在数轴上1,2之间或在1点,2点上时,x到1和2两点的距离和最小,|x-1|+|x-2|的最小值=2-1=1;
根据|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的几何意义,可得|x-1|+|x-2|+|x-3|+|x-4|+|x-5|表示x到数轴上1,2,3,4,5五个数的距离之和,
∴当x与3重合时,|x-1|+|x-2|+|x-3|+|x-4|+|x-5|有最小值,最小值为6,此时x=3.
故答案为:表示数1,2的点之间(包括1和2);1;6,3.
点评 本题主要考查了数轴以及数轴上两点间的距离公式的综合应用,解决问题的关键是掌握:在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.解题时注意:数轴上任意两点分别表示的数是a、b,则这两点间的距离可表示为|a-b|.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π)
如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com