
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() 的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
的图象于点A(2,﹣4)和点B(n,﹣2),交x轴于点C.
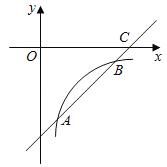
(1)求这两个函数的表达式;
(2)求△AOB的面积;
(3)请直接写出使一次函数值大于反比例函数值的x的范围.
【答案】(1)一次函数表达式为y=x﹣6;反比例函数的表达式是![]() ;(2)6;(3)0<x<2或x>4
;(2)6;(3)0<x<2或x>4
【解析】
(1)先把点A的坐标代入反比例函数表达式,从而的反比例函数解析式,再求点B的坐标,然后代入反比例函数解析式求出点B的坐标,再利用待定系数法求解即可;
(2)根据三角形的面积公式计算即可;
(3)观察函数图象即可求出不等式kx+b>![]() 的解集.
的解集.
解:(1)把A(2,﹣4)的坐标代入![]() 得:
得:![]() ,
,
∴4﹣2m=﹣8,反比例函数的表达式是![]() ;
;
把B(n,﹣2)的坐标代入![]() 得
得![]() ,
,
解得:n=4,
∴B点坐标为(4,﹣2),
把A(2,﹣4)、B(4,﹣2)的坐标代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数表达式为y=x﹣6;
(2)当y=0时,x=0+6=6,
∴OC=6,
∴△AOB的面积=![]() ×6×4﹣
×6×4﹣![]() ×6×2=6;
×6×2=6;
(3)由图象知,一次函数值大于反比例函数值的x的范围为0<x<2或x>4.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABN中,∠B =90°,点M是AB上的动点(不与A,B两点重合),点C是BN延长线上的动点(不与点N重合),且AM=BC,CN=BM,连接CM与AN交于点P.
(1)在图1中依题意补全图形;


(2)小伟通过观察、实验,提出猜想:在点M,N运动的过程中,始终有∠APM=45°.小伟把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的一种思路:
要想解决这个问题,首先应想办法移动部分等线段构造全等三角形,证明线段相等,再构造平行四边形,证明线段相等,进而证明等腰直角三角形,出现45°的角,再通过平行四边形对边平行的性质,证明∠APM=45°.
他们的一种作法是:过点M在AB下方作MD![]() AB于点M,并且使MD=CN.通过证明△AMD
AB于点M,并且使MD=CN.通过证明△AMD![]() △CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
△CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路,用另一种方法证明∠APM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
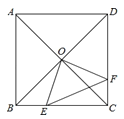
【题目】如图,正方形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,
,![]() 分别从
分别从![]() ,
,![]() 两点同时出发,以
两点同时出发,以![]() 的速度沿
的速度沿![]() ,
,![]() 运动,到点
运动,到点![]() ,
,![]() 时停止运动,设运动时间为
时停止运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A. B.
B.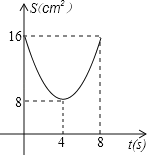 C.
C.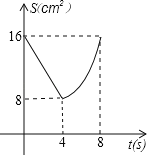 D.
D.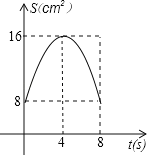
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论在数学中既是一个重要的策略思想又是一个重要的数学方法.例如对于像x2+|x|-6=0这样含有绝对值符号的方程,可采用如下的分类讨论方法:
解:当x≥0时,原方程可化为x2+x-6=0.
解得:x1=-3,x2=2.
∵x≥0,∴x=2.
当x<0时,原方程可化为x2-x-6=0,
解得:x1=3,x2=-2.
∵x<0,∴x=-2.
综上可得:原方程的解为x1=-2,x2=2.
仿照上面的解法,解方程:x2+|2x-1|-4=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
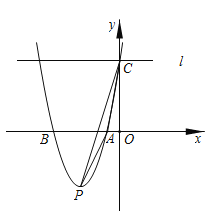
(1)求点![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的3倍?若存在,求出点
的面积的3倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
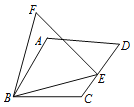
【题目】如图7,在四边形ABCD中,AB=BC,∠ABC=60°,E是CD边上一点,连接BE,以BE为一边作等边三角形BEF.请用直尺在图中连接一条线段,使图中存在经过旋转可完全重合的两个三角形,并说明这两个三角形经过什么样的旋转可重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A
(a>0,b<0)的图象与x轴只有一个公共点A
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中
中![]() ,
,![]() 的三条角平分线交于点
的三条角平分线交于点![]() ,过
,过![]() 作
作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
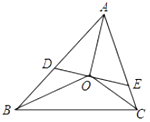
(1)写出图中的相似三角形(全等三角形除外),并选一对证明.
(2)若![]() ,
,![]() ,
,![]() 比
比![]() 长
长![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
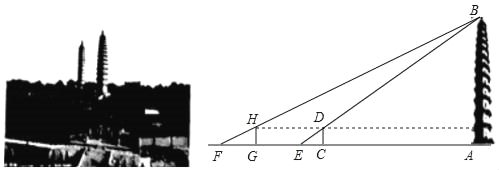
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com