
【题目】已知关于x的一元二次方程x2+bx+c=0.
(1)若b=2m﹣1,m+c=﹣6,判断方程根的情况;
(2)若方程有两个相等的非零实数根,且b2﹣c2﹣4=0,求此时方程的根.
【答案】(1)有两个不相等的实数根;(2)x1=x2=﹣![]()
【解析】
(1)由m+c=﹣6,可得出c=﹣m﹣6,根据方程的系数结合根的判别式,可得出△=4m2+25,结合m2≥0可得出△>0,进而可得出该方程有两个不相等的实数根;
(2)根据根的判别式△=0,即可得出b2=4c,结合b2﹣c2﹣4=0可得出b,c的值,再解一元二次方程即可得出结论.
解:(1)∵m+c=﹣6,
∴c=﹣m﹣6,
∴△=(2m﹣1)2﹣4×(﹣m﹣6)=4m2+25.
∵m2≥0,
∴4m2+25>0,即△>0,
∴该方程有两个不相等的实数根.
(2)∵方程有两个相等的实数根,
∴△=b2﹣4c=0,
∴b2=4c.
∵b2﹣c2﹣4=0,
∴b=±2![]() ,c=2,
,c=2,
当b=﹣2![]() ,c=2时,原方程为x2﹣2
,c=2时,原方程为x2﹣2![]() x+2=0,
x+2=0,
解得:x1=x2=![]() ;
;
当b=2![]() ,c=2时,原方程为x2+2
,c=2时,原方程为x2+2![]() x+2=0,
x+2=0,
解得:x1=x2=﹣![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】知识背景:当a>0且x>0时,因为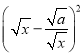 ≥0,所以
≥0,所以![]() ,从而
,从而![]() ≥
≥![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数![]() =
=![]() (
(![]() >0,x>0),由上述结论可知,当x=
>0,x>0),由上述结论可知,当x=![]() 时,该函数有最小值为
时,该函数有最小值为![]() .
.
应用举例:已知函数![]() =x(x>0)与函数
=x(x>0)与函数![]() =
=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,
=2时,![]() =
=![]() 有最小值为
有最小值为![]() =4.
=4.
解决问题:
(1)已知函数![]() =
=![]() (x>-3)与函数
(x>-3)与函数![]() =
=![]() (x>-3),当x为何值时,
(x>-3),当x为何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
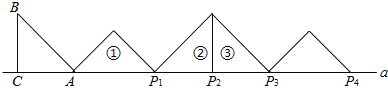
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,且AC边在直线a上,将
,且AC边在直线a上,将![]() 绕点A顺时针旋转到位置①可得到点
绕点A顺时针旋转到位置①可得到点![]() ,此时
,此时![]() ;将位置①的三角形绕点
;将位置①的三角形绕点![]() 顺时针旋转到位置②,可得到点
顺时针旋转到位置②,可得到点![]() ,此时
,此时![]() ;将位置②的三角形绕点
;将位置②的三角形绕点![]() 顺时针旋转到位置③,可得到点
顺时针旋转到位置③,可得到点![]() ,此时
,此时 ![]() ________,…,按此规律继续旋转,直至得到点
________,…,按此规律继续旋转,直至得到点![]() 为止,则
为止,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,割线ABC与⊙O相交于B、C两点,D为⊙O上一点,E为弧BC的中点,OE交BC于F,DE交AC于G,∠ADG=∠AGD.
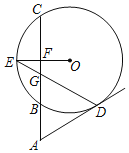
(1)求证明:AD是⊙D的切线;
(2)若∠A=60°,⊙O的半径为4,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过A(1,0)、B(﹣3,0),C(0,﹣3)三点,直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q.
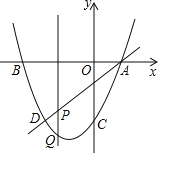
(1)求直线AD及抛物线的解析式;
(2)求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P、Q、D、R为顶点的四边形是平行四边形?若存在,求出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“完美四边形”.
(1)①在“平行四边形、梯形、菱形、正方形”中,一定不是“完美四边形”的有 ;
②若矩形ABCD是“完美四边形”,且AB=4,则BC= ;
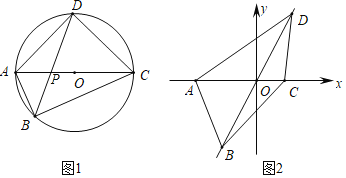
(2)如图1,“完美四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;
(3)如图2,平面直角坐标系中,已知“完美四边形”ABCD的四个顶点A(﹣3,0)、C (2,0),B在第三象限,D在第一象限,AC与BD交于点O,直线BD的斜率为![]() ,且四边形ABCD的面积为15
,且四边形ABCD的面积为15![]() ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(保留作图痕迹,不写做法)
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
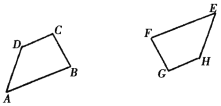
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.甲、乙两名同学被选中的概率各是多少?你认为这个规则公平吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com