
分析 (1)根据题意可知,这列数的规律是:分子为序数,分母比分子大1,序数为奇数时为负,序数为偶数时为正,即第n个数为(-1)n•$\frac{n}{n+1}$,据此解答即可;
(2)根据正负号交替分布即可得知;
(3)根据(1)中规律,写出第2014个数即可得.
解答 解:(1)∵-$\frac{1}{2}$,$\frac{2}{3}$,-$\frac{3}{4}$,$\frac{4}{5}$,-$\frac{5}{6}$,….
∴第n个数为(-1)n•$\frac{n}{n+1}$,
当n=100时,(-1)n•$\frac{n}{n+1}$=$\frac{100}{101}$,
当n=2015时,(-1)n•$\frac{n}{n+1}$=-$\frac{2015}{2016}$;
(2)由题意知前2014个数中,正数和负数个1007个,第2015个数为负数,
∴前2015个数中,正数有1007个、负数有1008个;
(3)$\frac{2014}{2015}$在这一列数中,
∵当n=2014时,(-1)n•$\frac{n}{n+1}$=$\frac{2014}{2015}$,
∴$\frac{2014}{2015}$在这一列数中.
点评 本题主要考查数字的变化规律,根据已知数列找出数字的变化部分及其变化的规律是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
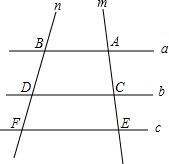 如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:
如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com