
 上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线
上,AC ⊥BC,且AC=BC;△EFP的边FP也在直线 上,边EF与边AC重合,且EF=FP.
上,边EF与边AC重合,且EF=FP. 向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论)
向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.猜想 BQ 与AP所满足的数量关系和位置关系。(直接写出结论) 向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)
向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.(6分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

| A.5m | B.12m | C.13m | D.18m |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
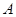 处6米处折断倒下,量得树梢
处6米处折断倒下,量得树梢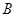 处与树底
处与树底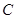 处的长是8米,树干
处的长是8米,树干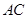 与地面
与地面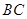 垂直.试通过计算求出这棵大树原来的高度.
垂直.试通过计算求出这棵大树原来的高度.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
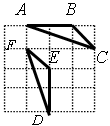
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.5 | B. | C.3 | D.4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com