
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
![]()
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论绝对值不等式|x|>3的解集为:x<-3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 .
②|x|<2.5的解集是 .
(2)求绝对值不等式2|x-3|+5>13的解集.
(3)直接写出不等式x2>4的解集是 .
【答案】(1)①x>1或x<-1;②-2.5<x<2.5;(2)x>7或x<-1;(3)x>2或x<-2.
【解析】
(1)先根据绝对值的定义,当|x|=1时,x=1或-1.再根据题意即可得;
(2)将2|x-3|+5>13化为|x-3|>4后,求出当|x-3|=4时,x=7或-1根据以上结论即可得;
(3)将x2>4化为|x|>2,再根据题意即可得.
解:(1)①根据绝对值的定义,当|x|=1时,x=1或-1,分界点把数轴分为三部分:
点-1左边的点表示的数的绝对值大于1;
点-1,1之间的点表示的数的绝对值小于1;
点1右边的点表示的数的绝对值大于1.
因此,绝对值不等式|x|>1的解集是 x>1或x<-1.
②根据绝对值的定义,当|x|=2.5时,x=2.5或-2.5,分界点把数轴分为三部分:
点-2.5左边的点表示的数的绝对值大于2.5;
点-2.5,2.5之间的点表示的数的绝对值小于2.5;
点2.5右边的点表示的数的绝对值大于2.5.
因此,绝对值不等式|x|<2.5的解集是-2.5<x<2.5.
故答案是:①x>1或x<-1;②-2.5<x<2.5;
(2)2|x-3|+5>13
∴2|x-3|>8
∴|x-3|>4
根据绝对值的定义,当|x-3|=4时,x=7或-1,分界点把数轴分为三部分:
点-1左边的点表示的数与3的差的绝对值大于4;
点-1,7之间的点表示的数与3的差的绝对值小于4;
点7右边的点表示的数与3的差的绝对值大于4
∴|x-3|>4的解集为x>7或x<-1;
∴2|x-3|+5>13的解集为x>7或x<-1;
(3)∵x2>4
∴|x|>2
根据绝对值的定义,当|x|=2时,x=2或-2,分界点把数轴分为三部分:
点-2左边的点表示的数的绝对值大于2;
点-2,2之间的点表示的数的绝对值小于2;
点2右边的点表示的数的绝对值大于2.
因此,绝对值不等式|x|>2的解集是 x>2或x<-2.
∴不等式x2>4的解集是 x>2或x<-2.
故答案是:x>2或x<-2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种泰山旅游纪念品,4月份的营业额为2000元,为扩大销售量,5月份该商店对这种纪念品打9折销售,结果销售量增加20件,营业额增加700元.
(1)求该种纪念品4月份的销售价格;
(2)若4月份销售这种纪念品获利800元,5月份销售这种纪念品获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,

(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下折痕EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
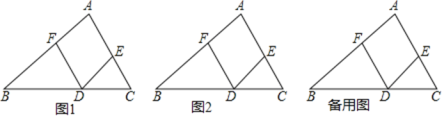
【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
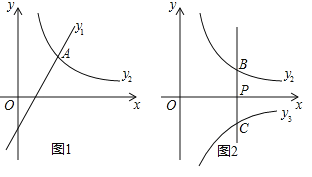
![]() 如图1,若
如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .求m,k的值;
.求m,k的值;
![]() 如图2,过点
如图2,过点![]() 作y轴的平行线l与函数
作y轴的平行线l与函数![]() 的图象相交于点B,与反比例函数
的图象相交于点B,与反比例函数![]() 的图象相交于点C.
的图象相交于点C.
![]() 若
若![]() ,直线l与函数
,直线l与函数![]() 的图象相交点
的图象相交点![]() 当点B、C、D中的一点到另外两点的距离相等时,求
当点B、C、D中的一点到另外两点的距离相等时,求![]() 的值;
的值;
![]() 过点B作x轴的平行线与函数
过点B作x轴的平行线与函数![]() 的图象相交与点
的图象相交与点![]() 当
当![]() 的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
查看答案和解析>>
科目:初中数学 来源: 题型:
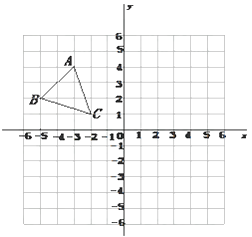
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别 A(-3,4)B(-5,2)C(-2,1)
(1)画出 △ABC关于y 轴的对称图形 △A1B1C1;
(2)画出将△ABC 绕原点 O逆时针方向旋转90°得到的△A2B2C2 ;
(3)求(2)中线段 OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC:
(1)求作△ABC的内切圆⊙O,与边AB、BC、AC分别相切于点D、E、F;
(2)若AB=6,BC=8,AC=12,求AD、BE、CF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com