
����Ŀ�����Ϲ����Ѿ���Ϊ���dz��õ�һ�ֹ��﷽ʽ���ۺ������ر����˹�ע�������������깺��ij����Ʒ������
�����������������������������������ۣ����������������ǵȿ��ܵģ�
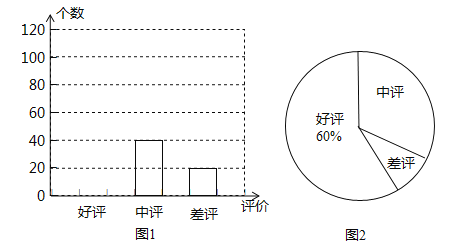
��1��С����һ����������ij����Ʒ��ʾ��������Ϣ������ͳ�ƣ����г���������������ͳ��ͼ��
����ͼ�����ṩ����Ϣ����������⣺
��С��һ��ͳ���� �����ۣ�
���뽫ͼ1����������
��ͼ2������������ռ�İٷֱ��� ��
��2�����ס��������������ڸ����깺����ͬһ��Ʒ���������б������״ͼ�ķ�������������һ��������������һ�������������ĸ��ʣ�
���𰸡���1����150������ͼ����������13.3%����2��![]() ��
��
��������
��1���������������������������������Զ��ߵİٷֱ�֮�ͼ��ɵ���������������������ȥ�������������������������ɵ�������������������ȫ����ͼ���ɣ�������������������������������100%���ɵ�����������ռ�İٷֱȣ�
��2����ͨ���б���ʾ���ס��Ҷ���Ʒ���۵����п��ܽ���������ݸ��ʹ�ʽ���ɼ����������������һ�������������ĸ��ʣ�
��С��ͳ�Ƶ�����һ���У���40+20������1-60%=150��������
�ڡ�������һ����150��60%=90����������ȫ����ͼ��ͼ1��
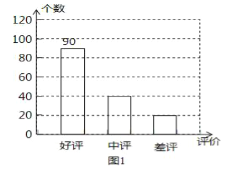
��ͼ2������������ռ�İٷֱ��ǣ�![]() ��100%=13.3%��
��100%=13.3%��
��2���б����£�
�� | �� | �� | |
�� | ��� | ��� | ��� |
�� | ���� | ���� | ���� |
�� | ��� | ��� | ��� |
�ɱ���֪��һ����9�ֵȿ��ܽ��������������һ����������������5�֣�
��������������һ�������������ĸ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
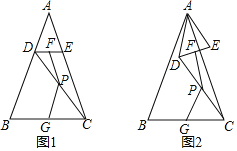
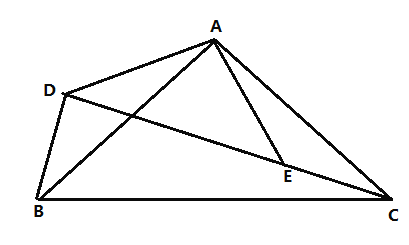
����Ŀ����ͼ1���ڡ�ABC�У�AB��AC����BAC��������D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������DC����F��P��G�ֱ�ΪDE��DC��BC���е㣮
��1���۲���룺ͼ1�У��߶�PF��PG��������ϵ���� ����FPG���� ���ú����Ĵ���ʽ��ʾ��
��2��̽��֤��������ADE�Ƶ�A��ת����ͼ2��ʾ��λ��ʱ��С�²��루1���еĽ�����Ȼ����������֤��С�µIJ��룮
��3����չ���죺�ѡ�ADE�Ƶ�A��ƽ����������ת����AD��2��AB��6����ֱ��д��PF�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
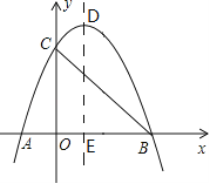
����Ŀ����ͼ��������![]() ��x�ύ�ڵ�A(-1��0)��B(3��0)����y����������ڵ�C���Գ��ύ�������ڵ�D����x�����E�������н��ۣ���2a+b=0����b+2c>0����a+b>am
��x�ύ�ڵ�A(-1��0)��B(3��0)����y����������ڵ�C���Գ��ύ�������ڵ�D����x�����E�������н��ۣ���2a+b=0����b+2c>0����a+b>am![]() +bm��mΪ����ʵ��������һԪ���η���
+bm��mΪ����ʵ��������һԪ���η���![]() ����������ȵ�ʵ�������ݵ���BCDΪֱ��������ʱ��a��ֵ��2����������PΪ�Գ����ϵĶ��㣬��
����������ȵ�ʵ�������ݵ���BCDΪֱ��������ʱ��a��ֵ��2����������PΪ�Գ����ϵĶ��㣬��![]() �����ֵ�����ֵΪ
�����ֵ�����ֵΪ![]() ��������ȷ���У� ��
��������ȷ���У� ��
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60���õ���CBD������B������Ϊ��2�� 0�������C������Ϊ�� ��
������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60���õ���CBD������B������Ϊ��2�� 0�������C������Ϊ�� ��

A.����1��![]() ��B.����2��
��B.����2��![]() ��C.��
��C.��![]() ��1��D.��
��1��D.��![]() ��2��
��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
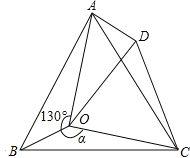
����Ŀ����ͼ����O�ǵȱ�������ABC�ڵ�һ�㣬��AOB=130�㣬��BOC=��������BOC�Ƶ�C��˳ʱ�뷽����ת60���õ���ADC������OD��
��1���жϡ�COD����״��������˵�����ɣ�
��2����AD=1��OC=![]() ��OA=
��OA=![]() ʱ�������Ķ�����
ʱ�������Ķ�����
��3��̽��������Ϊ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ܵ�ѧУʳ��������A��B������ǰ���Ŷӵ���һ����(��Ϊa�ˣ�a��8������վ��A���ڶ���ĺ��棬����2���ӣ�������A����ÿ������4�����˷��뿪���飬B����ÿ������6�����˷��뿪���飬��B���ڶ������ÿ��������5�ˣ�
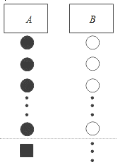
��1����ʱ����С�ܼ�����A�����Ŷӣ��������ﴰ��������ʱ���Ƕ��٣����ú�a�Ĵ���ʽ��ʾ��
��2����ʱ����С��Ѹ�ٴ�A���ڶ���ת�Ƶ�B���ں��������Ŷӣ��ҵ���B����������ʱ��ȼ�����A�����Ŷӵ���A����������ʱ���٣���a��ȡֵ��Χ�����������������أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��ѧ��С��Ҹ�����һ���������̻�����ʾ��ͼ��Ϊ��ǿ���ʣ���ÿ���糿�������̻����ܱ�С·AB��BC��CA�ܲ�
��ѧ��С��Ҹ�����һ���������̻�����ʾ��ͼ��Ϊ��ǿ���ʣ���ÿ���糿�������̻����ܱ�С·AB��BC��CA�ܲ�![]() С·�Ŀ��Ȳ���
С·�Ŀ��Ȳ���![]() �۲�õ�B�ڵ�A����ƫ��
�۲�õ�B�ڵ�A����ƫ��![]() �����ϣ���C�ڵ�A����ƫ��
�����ϣ���C�ڵ�A����ƫ��![]() �ķ����ϣ���B�ڵ�C�ı�ƫ��
�ķ����ϣ���B�ڵ�C�ı�ƫ��![]() �����ϣ�AC�����Ϊ400��
�����ϣ�AC�����Ϊ400��![]() ��С�����������̻������ܱ�С·��һȦ�����˶����ף�
��С�����������̻������ܱ�С·��һȦ�����˶����ף�
![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
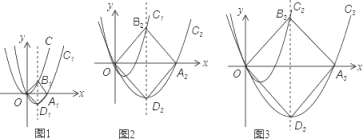
����Ŀ����ͼ1��������C��y��x2�����任�ɵõ�������C1��y1��a1x��x��b1����C1��x��������ύ�ڵ�A������Գ���ֱ�������C��C1�ڵ�B1��D1����ʱ�ı���OB1A1D1ǡΪ�����Σ����������Ʒ�������ͼ2��������C1��y1��a1x��x��b1�������任�ɵõ�������C2��y2��a2x��x��b2����C2��x��������ύ�ڵ�A2������Գ���ֱ�������C1��C2�ڵ�B2��D2����ʱ�ı���OB2A2D2ҲǡΪ�����Σ����������Ʒ�������ͼ3���ɵõ�������C3��y3��a3x��x��b3����������OB3A3D3����̽���������⣺
��1����գ�a1���� ��b1���� ��
��2�����C2��C3�Ľ���ʽ��
��3�����������Ʒ������ɵõ�������n��yn��anx��x��bn����������OBnAnDn��n��1��
�����ú�n�Ĵ���ʽֱ�ӱ�ʾ��n�Ľ���ʽ��
�ڵ�xȡ���ⲻΪ0��ʵ��ʱ���ԱȽ�y2018��y2019�ĺ���ֵ�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��![]() ��
��![]() ��Ϊ����ֱ�������Σ�
��Ϊ����ֱ�������Σ�![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ������һֱ���ϣ�
������һֱ���ϣ�![]() ��
��![]() ��
��
��1����֤��![]() ��
��
��2�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com