
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
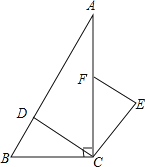
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
【答案】(1)见解析;(2)90°
【解析】
试题分析:(1)由旋转的性质可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;
(2)由(1)可知:△BCD≌△FCE,所以∠BDC=∠E,易求∠E=90°,进而可求出∠BDC的度数.
(1)证明:∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°﹣∠ACD=∠FCE,
在△BCD和△FCE中,
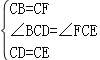 ,
,
∴△BCD≌△FCE(SAS).
(2)解:由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°﹣∠DCE=90°,
∴∠BDC=90°.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
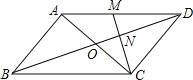
(1)求BD的长;
(2)在直线AC的同侧,以点O为位似中心,作出△CON的位似三角形,并使△CON与和它位似的三角形的位似比是1:2.(写出结果,不写作法,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
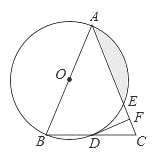
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯水价”的有关文件要求,某市结合地方实际,决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费,某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量,如表所示:
用水量(吨) | 15 | 20 | 25 | 30 | 35 |
户数 | 3 | 6 | 7 | 9 | 5 |
则这30户家庭该用用水量的众数和中位数分别是( )
A.25,27 B.25,25 C.30,27 D.30,25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:如图1,直线a,b被直线c所截,且∠1+∠2=180°.求证:a∥b.
(2)如图2,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
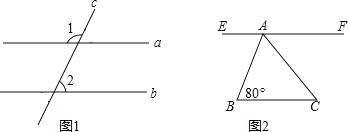
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】判断题
(1)不相交的两条直线叫做平行线.( )
(2)在同一平面内,不相交的两条射线是平行线.( )
(3)如果一条直线与两条平行线中的一条平行, 那么它与另一条也互相平行.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com