
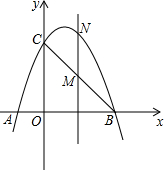 ��ͼ����֪�����߾�����A��-1��0����B��3��0����C��0��3�����㣮
��ͼ����֪�����߾�����A��-1��0����B��3��0����C��0��3�����㣮���� ��1���������߹���A��B����������ߵĽ���ʽΪy=a��x+1����x-3���������C�����꼴�����aֵ���Ӷ��ó������ߵĽ���ʽ��
��2��������ڣ����ݵ�B��C���������ô���ϵ���������ֱ��BC�Ľ���ʽ�����ݵ�M�ĺ�����m���ú�m�Ĵ���ʽ��ʾ����M��N�����꣬ͨ���ָ�������������������ú�m�Ķ��κ�����ʾ����BNC������������ö��κ��������ʼ��ɽ����ֵ���⣻
��3����ϣ�2���ҳ���M��N�����꣬����C��CG��ND�ڵ�G���ֵ�F���߶�NG��DG�����������t��ֵ���ٵ���F���߶�NG��ʱ����ͨ�����ɶ������t�����ֵ���ڵ���F���߶�DG��ʱ��ͨ�����������ε������ҳ�t����Сֵ�����ϼ��ɵó����ۣ�
��� �⣺��1���������߾�����A��-1��0����B��3��0����
����������ߵĽ���ʽΪy=a��x+1����x-3����
����C��0��3������y=a��x+1����x-3���еã�
3=a����0+1����0-3������ã�a=-1��
��������ߵĽ���ʽΪy=-��x+1����x-3��=-x2+2x+3��
��2��������ڣ���ֱ��BC�Ľ���ʽΪy=kx+b��
�ߵ�B��3��0����C��0��3����ֱ��y=kx+b�ϣ�
����$\left\{\begin{array}{l}{0=3k+b}\\{3=b}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-x+3��
�ߵ�M�ĺ�����Ϊm��MN��y�ᣬ
���M��������m��3-m����0��m��3������N��������m��-m2+2m+3����
���߶�MN=-m2+2m+3-��3-m��=-m2+3m��
S��BNC=$\frac{1}{2}$MN•OB=-$\frac{3}{2}$m2+$\frac{9}{2}$m=-$\frac{3}{2}$$��m-\frac{3}{2}��^{2}$+$\frac{27}{8}$��
�൱m=$\frac{3}{2}$ʱ��S��BNCȡ���ֵ�����ֵΪ$\frac{27}{8}$��
�ʴ���m��ʹ��BNC��������ʱm=$\frac{3}{2}$��S��BNC�����ֵΪ$\frac{27}{8}$��
��3��������ڣ�
�ɣ�2����֪����M��N�ĺ�����Ϊ$\frac{3}{2}$���ֱ����y=-x+3��y=-x2+2x+3�У�
�õ�M������Ϊ��$\frac{3}{2}$��$\frac{3}{2}$������N������Ϊ��$\frac{3}{2}$��$\frac{15}{4}$����
����C��CG��ND�ڵ�G��
�ٵ���F���߶�NG��ʱ����F���N�غ�ʱ����E�ĺ����������ͼ1��ʾ��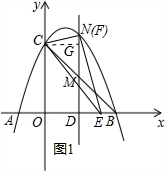
�������ľ��빫ʽ��֪��
CF2=$��\frac{3}{2}-0��^{2}+��\frac{15}{4}-3��^{2}$=$\frac{45}{16}$��EF2=$��t-\frac{3}{2}��^{2}+��0-\frac{15}{4}��^{2}$=t2-3t+$\frac{261}{16}$��EC2=��t-0��2+��0-3��2=t2+9��
��Rt��EFC��CF2+EF2=EC2����$\frac{45}{16}$+t2-3t+$\frac{261}{16}$=t2+9��
��ã�t=$\frac{27}{8}$����t�����ֵΪ$\frac{27}{8}$��
�ڵ���F���߶�DG��ʱ����ͼ2��ʾ��
��FG=x��0��x��3������DF=3-x��
����ͬ�ǵ������ȣ��á�FCG=��EFD��
���FCG�ס�EFD��
��$\frac{FG}{ED}=\frac{CG}{FD}$����$\frac{x}{DE}=\frac{\frac{3}{2}}{3-x}$��
��DE=$\frac{2}{3}$x��3-x��=-$\frac{2}{3}$$��x-\frac{3}{2}��^{2}$+$\frac{3}{2}$��
�൱x=$\frac{3}{2}$ʱ��DEȡ���ֵ$\frac{3}{2}$����ʱ��Ӧ��tֵ��С����СֵΪ0��
���Ͽ�֪������BNC��������ʱ������t��ʹ��EFC=90�㣬t��ȡֵ��ΧΪ0��t��$\frac{27}{8}$��
���� ���⿼���˴���ϵ������������ʽ�����κ��������ʡ��ָ�ͼ�η�������Լ����ɶ���������Ĺؼ��ǣ���1�����ô���ϵ���������������ʽ����2�����÷ָ�ͼ�η��������ε��������3�������Ѱ��t����ֵ�����������е��⣬��1����2����Լ���3���е��Ѷȣ��ٽ������ʱ��ͨ���ֶ�Ѱ���ٽ�㣬���tֵ���������Сֵ���Ӷ��ó�t��ȡֵ��Χ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
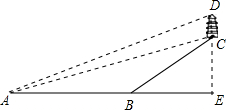 ���빫˾�����������˽���֣�ǰ��Ϊ��Բ���ǹ��Ҽ�AAA���ξ�����Բ����һ��ʤ¥�����ϸ�¥�����͵������������ɫ����ĩС��ͬѧ�������빫˾����ͼ����A�㴦�۲쵽��ʤ¥¥��C������Ϊ12�㣬¥��D������Ϊ13�㣬���ˮƽ����AE=1200m��BC���¶�i=8��15
���빫˾�����������˽���֣�ǰ��Ϊ��Բ���ǹ��Ҽ�AAA���ξ�����Բ����һ��ʤ¥�����ϸ�¥�����͵������������ɫ����ĩС��ͬѧ�������빫˾����ͼ����A�㴦�۲쵽��ʤ¥¥��C������Ϊ12�㣬¥��D������Ϊ13�㣬���ˮƽ����AE=1200m��BC���¶�i=8��15�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
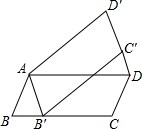 ��ͼ����ƽ���ı���ABCD�Ƶ�A��ʱ����ת40�㣬�õ�ƽ���ı���AB��C��D�䣬����B��ǡ������BC���ϣ����DC��B��Ķ���Ϊ��������
��ͼ����ƽ���ı���ABCD�Ƶ�A��ʱ����ת40�㣬�õ�ƽ���ı���AB��C��D�䣬����B��ǡ������BC���ϣ����DC��B��Ķ���Ϊ��������| A�� | 60�� | B�� | 65�� | C�� | 70�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
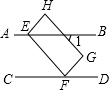 ��ͼ��AB��CD��������EFGH�Ķ���E��F�ֱ����ֱ��AB��CD�ϣ�����1=40�㣬���CFG�Ķ�������130�㣮
��ͼ��AB��CD��������EFGH�Ķ���E��F�ֱ����ֱ��AB��CD�ϣ�����1=40�㣬���CFG�Ķ�������130�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
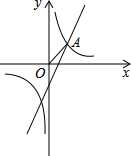 ��ͼ����֪��A�Ƿ���������y=$\frac{1}{x}$��ͼ����һ�κ���y=2x-1��ͼ���ڵ�һ���Ľ��㣬��P��x����һ�㣬����OAPΪ����������ʱ����P������Ϊ��$\sqrt{2}$��0������-$\sqrt{2}$��0������2��0������1��0����
��ͼ����֪��A�Ƿ���������y=$\frac{1}{x}$��ͼ����һ�κ���y=2x-1��ͼ���ڵ�һ���Ľ��㣬��P��x����һ�㣬����OAPΪ����������ʱ����P������Ϊ��$\sqrt{2}$��0������-$\sqrt{2}$��0������2��0������1��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1=y2 | C�� | y1��y2 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com