

分析 (1①由角平分线定义得出∠AOP=∠BOP=24°,再由平行线的性质得出∠OCB=∠AOP=24°即可;
②由三角形内角和定理求出∠CBD=78°,再由平行线的性质得出∠EAB=102°即可;
(2)分两种情况:①点D在线段OC上时,求出∠OBC=66°,由已知条件证出△CDB是等腰直角三角形,得出∠CBD=∠CDB=45°,求出∠OBD=21°,由三角形的外角性质得出∠EAB=∠EOF+∠OBD,即可得出结果;
②点D在射线OC上时,由①得:∠OBD=∠OBC+∠CBD=111°,再由三角形的外角性质即可得出结果.
解答 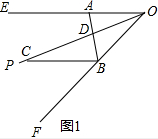 解:(1①如图1:∵∠EOF=48°,OP平分∠EOF,
解:(1①如图1:∵∠EOF=48°,OP平分∠EOF,
∴∠AOP=∠BOP=24°
∵BC∥AE,
∴∠OCB=∠AOP=24°;
故答案为:24;
②∵∠CDB=∠CBD,∠OCB=24°,
∴∠CBD=(180°-24°)÷2=78°,
∵BC∥OE,
∴∠EAB+∠CBD=180°,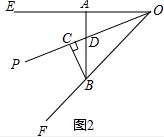
∴∠EAB=180°-78°=102°,
即α=102°;
(2)存在这样的α,使得△CDB中有两个内角相等,α为69°或159°.理由如下:
分两种情况:
①点D在线段OC上时,如图2所示:
∵CB⊥OP,
∴∠OCB=90°,
∵∠BOP=24°,
∴∠OBC=90°-24°=66°,
∵△CDB中有两个内角相等,
∴△CDB是等腰直角三角形,
∴∠CBD=∠CDB=45°,
∴∠OBD=66°-45°=21°,
∴∠EAB=∠EOF+∠OBD=48°+21°=69°,
即α=69°;
②点D在射线OC上时,如图3所示:
由①得:∠OBD=∠OBC+∠CBD=66°+∠45°=111°,
∴∠EAB=∠EOF+∠OBD=48°+111°=159°,
即α=159°;
综上所述:存在这样的α,使得△CDB中有两个内角相等,α为69°或159°.
点评 本题是三角形综合题目,考查了平行线的性质、角平分线定义、等腰直角三角形的判定与性质、三角形的内角和定理和三角形的外角性质的应用;熟练掌握三角形内角和定理和三角形的外角性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 种类 | 标价 | 优惠方案 |
| A品牌足球 | 150元/个 | 八折 |
| B品牌足球 | 100元/个 | 九折 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合,试写出重叠部分面积y(cm2)与MA长度x(cm)之间的函数关系式(指出自变量取值范围)是y=$\frac{1}{2}$x2 (0<x≤10)..
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合,试写出重叠部分面积y(cm2)与MA长度x(cm)之间的函数关系式(指出自变量取值范围)是y=$\frac{1}{2}$x2 (0<x≤10)..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com