
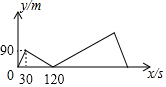
 甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇.
甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后$\frac{360}{7}$秒与甲相遇. 分析 根据速度=路程÷时间可求出甲的速度,由乙的速度=甲的速度+二者速度差可求出乙的速度,利用时间=路程÷速度可求出乙到达终点的时间,结合路程=速度×时间可求出此时甲离终点的距离,再根据相遇所需时间=甲离终点的距离÷甲、乙速度和,即可得出结论.
解答 解:甲的速度为90÷30=3(米/秒),
乙的速度为3+90÷(120-30)=4(米/秒).
乙到达终点时,甲出发的时间为1800÷4+30=480(秒),
此时甲离终点的距离为1800-3×480=360(米),
乙返回后与甲相遇的时间为360÷(3+4)=$\frac{360}{7}$(秒).
故答案为:$\frac{360}{7}$.
点评 本题考查了一次函数的应用,根据数量关系结合图象列式计算是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④.
平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD,AB的中点.下列结论:①EG=EF; ②△EFG≌△GBE; ③FB平分∠EFG;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$$-\sqrt{3}$=2$\sqrt{3}$ | B. | -2+|-2|=0 | C. | x2•x3=x6 | D. | (-3)2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com