练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，直线y=
    1
    2
    x+5    与x轴，y轴分别交于A，B两点，点M为直线AB上一个动点，点N在x轴上方的坐标平面内，若以M，N，O，B为顶点的四边形是菱形，则N的坐标为______．
    ①当OB为菱形的对角线时，如图1，由OB=5可知，M点纵坐标为
    5
    2
    ，
    代入直线y=
    1
    2
    x+5    中，得M点横坐标为-5，
    ∵M、N关于y轴对称，∴N（5，
    5
    2
    ）；

    ②当OB为菱形的边时，如图2，
    延长MN交x轴于P点，
    ∵OA=10，OB=5，
    ∴AB=
    		OA2+OB2
    =5
    		5
    ，
    而ON=5，由△OPN∽△AOB，
    得
    OP
    AO
    =
    PN
    OB
    =
    ON
    AB
    ，即
    OP
    10
    =
    PN
    5
    =
    5
    5
    		5
    ，
    解得OP=2
    		5
    ，PN=
    		5
    ，
    ∴N（2
    		5
    ，
    		5
    ），
    同理可得N′（-4，8）．

    故答案为：（2
    		5
    ，
    		5
    ）（-4，8）（5，
    5
    2
    ）．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    “城市发展交通先行”，成都市今年在中心城区启动了缓堵保畅的二环路高架桥快速通道建设工程，建成后将大大提升二环路的通行能力．研究表明，某种情况下，高架桥上的车流速度V（单位：千米/时）是车流密度x（单位：辆/千米）的函数，且当0＜x≤28时，V=80；当28＜x≤188时，V是x的一次函数．函数关系如图所示．
    （1）求当28＜x≤188时，V关于x的函数表达式；
    （2）若车流速度V不低于50千米/时，求当车流密度x为多少时，车流量P（单位：辆/时）达到最大，并求出这一最大值．
    （注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，在直角梯形OABC中，AB∥OC，过点O、点B的直线解析式为y=
    4
    3
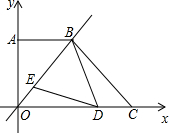    x，OA、AB是方程x2-14x+48=0的两个根，OB=BC，D、E分别是线段OC、OB上的动点（点D与点O、点C不重合），且∠BDE=∠ABO，设CD=x，BE=y．
    （1）求BC和OC的长；
    （2）求y与x的函数关系式；
    （3）是否存在x的值，使以点B、点D、点E为顶点的三角形为等腰三角形？若存在，请直接写出x的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    弹簧的长度y（cm）与所挂物体的质量x（kg）关系如右图所示，刚弹簧不挂重物时的长度是（　　）
    A．9cmB．10cmC．10.5cmD．11cm

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，Rt△ABC中，∠ABC=90°，OA=OB=1，与x轴的正方向夹角为30°．求直线AB的解析式．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    暑假期间，王红随爸爸妈妈到一个著名森林风景区旅游，导游提醒大家上山要多带一件衣服，并介绍山区气温会随着海拔高度的增加而下降，沿途王红利用随身带的登山表（具有测定当前位置的海拔高度和气温等功能）测得以下的数据：
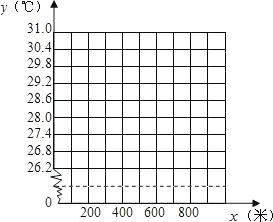
    海拔高度x（米）300400500600700…
    气温y（℃）29.228.628.027.426.8…
    （1）设海拔高度为x（米），气温为y（℃），根据上表提供的数据在下列直角坐标系中描点并连线；
    （2）观察（1）中所画出的图象，猜想y与x之间函数关系，求出所猜想的函数关系表达式；
    （3）如果王红到达山顶时，只告诉你山顶的气温为20.2℃，请计算此风景区山顶海拔高度大约是多少米？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    看图填空：
    （1）当y=0时，x=______；
    （2）直线对应的函数表达式是______．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

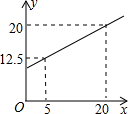
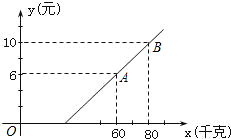    某长途客运公司规定每位旅客可以免费托运一定重量的行李，超过部分则需缴交行李托运费．行李费托运费y（元）与行李重量x（千克）之间的函数关系如图所示．
    （1）求y与x的函数关系式；
    （2）每位旅客最多可以免费托运多少千克行李？
    （3）某旅客行托运行李100千克，应交多少行李托运费？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    已知一个直角三角形纸片OAB，其中∠AOB=90°，OA=2，OB=4．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB交于点C，与边AB交于点D．

    （1）若折叠后使点B与点O重合，则点C的坐标为______；若折叠后使点B与点A重合，则点C的坐标为______；
    （2）若折叠后点B落在边OA上的点为B′，设OB′=x，OC=y，试写出y关于x的函数解析式，并确定y的取值范围；
    （3）若折痕经过点O，请求出点B落在x轴上的点B′的坐标；
    （4）若折叠后点B落在边OA上的点为B′，且使DB′⊥OA，求此时点C的坐标．

    查看答案和解析>>

    同步练习册答案