
 )
)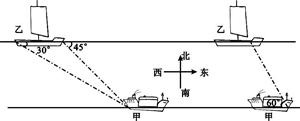
 米,则乙船长度CD=(120
米,则乙船长度CD=(120 -120)≈88米.再过A′作A′E⊥CD于E,由A′E=120米,得出D′E=40
-120)≈88米.再过A′作A′E⊥CD于E,由A′E=120米,得出D′E=40 米.又AA′=600×
米.又AA′=600× =300(米),则HE=BA′=320米,乙船从D到D′走了(440-40
=300(米),则HE=BA′=320米,乙船从D到D′走了(440-40 )米,用时30秒=
)米,用时30秒= 分,然后根据速度=路程÷时间即可求解.
分,然后根据速度=路程÷时间即可求解.
 米,
米, -120)≈88米.
-120)≈88米. 米.
米. =300(米),
=300(米), )米,用时30秒=
)米,用时30秒= 分,
分, )÷
)÷ =(880-80
=(880-80 )≈742米/分.
)≈742米/分.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N. 时,求
时,求 的值;
的值; 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
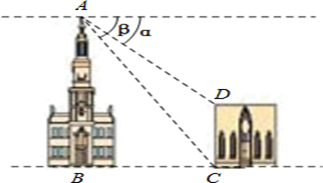
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 B.
B.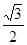 C.
C.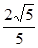 D.
D.
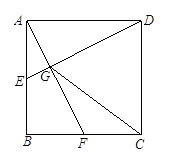
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
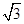 ,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )
,点P、H、B、C、A在同一个平面上的点H、B、C在同一条直线上,且PH⊥HC.则A、B两点间的距离是( )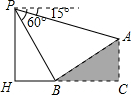
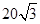 C.
C.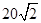 D.
D.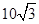
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
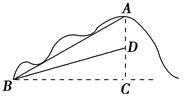
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
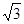 千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.
千米到达B地,然后再沿北偏西45°方向行进了5千米到达目的地点C.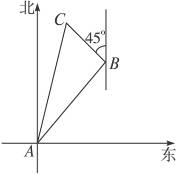
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com