
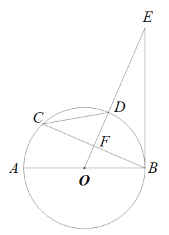
【题目】如图,AB是⊙O的直径, OE垂直于弦BC,垂足为F,OE交⊙O于点D,且∠CBE=2∠C.
(1)求证:BE与⊙O相切;
(2)若DF=9,tanC=![]() ,求直径AB的长.
,求直径AB的长.
【答案】(1)见解析;(2)25
【解析】
(1)由OE垂直于弦BC,可证∠BOE+∠OBF=90°,由圆周角定理可得∠BOE=2∠C,从而∠CBE=∠BOE,进而可证BE与⊙O相切;
(2)由DF=9,tanC=![]() ,可求出CF=BF=12,设半径长是x,在Rt△BOF中,利用勾股定理列方程求解即可.
,可求出CF=BF=12,设半径长是x,在Rt△BOF中,利用勾股定理列方程求解即可.
(1)证明:∵OE垂直于弦BC,
∴∠BOE+∠OBF=90°,
∵∠CBE=2∠C, ∠BOE=2∠C,
∴∠CBE=∠BOE,
∴∠CBE+∠OBF=90°,
∴∠OBE=90°,
∴BE与⊙O相切;
(2)解:∵OE垂直于弦BC,
∴∠CFD=∠BFO=90°,CF=BF.
∵DF=9,tanC=![]() ,
,
∴CF=BF=12.
设半径长是x,则OF=x-9,
在Rt△BOF中,
∵x2=(x-9)2+122,
∴x=![]() ,
,
∴直径AB=25.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,以点
,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() ,分别交直线
,分别交直线![]() 和
和![]() 轴于
轴于![]() ,
,![]() 两点,以点
两点,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,…,按此规律进行下去,则点
,…,按此规律进行下去,则点![]() 的坐标为__________ (结果用含正整数
的坐标为__________ (结果用含正整数![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
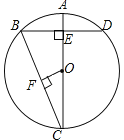
A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A逆时针旋转得到△ADE,其中点B、C分别与点D、E对应,如果B、D、C三点恰好在同一直线上,那么下列结论错误的是( )
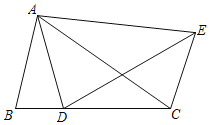
A.∠ACB=∠AEDB.∠BAD=∠CAE
C.∠ADE=∠ACED.∠DAC=∠CDE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. 14SB. 13SC. 12SD. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com