
如图,在平面直角坐标系中,直线 =
= 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以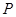 为圆心,3为半径作
为圆心,3为半径作 .
.
(1)连结 ,若
,若 ,试判断
,试判断 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当 为何值时,以
为何值时,以 与直线
与直线 =
= 的两个交点和圆心
的两个交点和圆心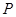 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
(1)⊙P与x轴相切.理由见解析;(2) -8或k=-
-8或k=- -8
-8
解析试题分析:(1)通过一次函数可求出A、B两点的坐标及线段的长,再在Rt△AOP利用勾股定理可求得当PB=PA时k的值,再与圆的半径相比较,即可得出⊙P与x轴的位置关系.
(2)根据正三角形的性质,分两种情况讨论,
①当圆心P在线段OB上时,②当圆心P在线段OB的延长线上时,从而求得k的值.
试题解析:(1)⊙P与x轴相切,
∵直线y=-2x-8与x轴交于A(-4,0),与y轴交于B(0,-8),
∴OA=4,OB=8.
由题意,OP=-k,
∴PB=PA=8+k.
∵在Rt△AOP中,k2+42=(8+k)2
∴k=-3,
∴OP等于⊙P的半径.
∴⊙P与x轴相切.
(2)设⊙P1与直线l交于C,D两点,连接P1C,P1D,
当圆心P1在线段OB上时,作P1E⊥CD于E,
∵△P1CD为正三角形,
∴DE= CD=
CD= ,P1D=3.
,P1D=3.
∴P1E= .
.
∵∠AOB=∠P1EB=90°,∠ABO=∠P1BE,
∴△AOB∽△P1EB.
∴ ,即
,即 ,
,
∴P1B= .
.
∴P1O=BO-BP1=8- .
.
∴P1(0, -8).
-8).
∴k= -8.
-8.
当圆心P2在线段OB延长线上时,同理可得P2(0,- -8).
-8).
∴k=- -8.
-8.
∴当k= -8或k=-
-8或k=- -8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
考点:1.切线的判定;2.一次函数图象上点的坐标特征;3.等边三角形的性质;4.勾股定理;5.相似三角形的判定与性质.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
如图,在△PAB中,点C、D在边AB上,PC=PD=CD,∠APB=120°.
(1)试说明△APC与△PBD相似.
(2)若CD=1,AC=x,BD=y,请你求出y与x之间的函数关系式.
(3)小明猜想:若PC=PD=1,∠CPD=α,∠APB=β,只要α与β之间满足某种关系式,问题(2)中的函数关系式仍然成立.你同意小明的观点吗?如果你同意,请求出α与β所满足的关系式;若不同意,请说明理曲.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC,△A1B1C1.
(1)将△ABC,△A1B1C1如图②摆放,使点A1与B重合,点B1在AC边的延长线上,连接CC1交BB1于点E.
①求证:四边形C1B1AB为梯形.
②若∠A="45°," ∠ABC="30°," 求∠B1C1C的度数
(2)若将△ABC,△A1B1C1如图③摆放,使点B1与B重合,点A1在AC边的延长线上,连接CC1交A1B于点F.试判断∠A1C1C与∠A1BC是否相等,并说明理由.
(3)在(2)的条件下,若AC=3,B1C1=6,设A1B=x,C1F=y,写出y与x的函数关系式(不要求写出自变量的取值范围)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在□ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在梯形ABCD中,AB∥CD,∠DAB=90°,AC⊥BC.
(1)求证:△ADC∽△BCA;
(2)若AB=9cm,AC=6cm,求梯形ABCD中位线的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com