
 如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π)
如图,AB是⊙O的切线,半径OA=2,OB交⊙O于C,∠B=30°,则阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(结果保留π) 分析 根据阴影部分的面积=△OAB的面积-扇形AOC的面积计算即可.
解答 解:
∵AB是⊙O的切线,
∴OA⊥AB,
∵OA=2,∠B=30°,
∴OB=4,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=2$\sqrt{3}$,∠O=60°,
∴阴影部分的面积=△OAB的面积-扇形AOC的面积=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{30π×4}{360}$=2$\sqrt{3}$-$\frac{1}{3}$π,
故答案为:2$\sqrt{3}$-$\frac{1}{3}$π.
点评 本题考查的是切线的性质、扇形面积的计算,掌握切线的性质定理、扇形的面积公式是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:选择题

| A. | 1344+672$\sqrt{2}$ | B. | 1344+673$\sqrt{2}$ | C. | 1345+673$\sqrt{2}$ | D. | 1345+674$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
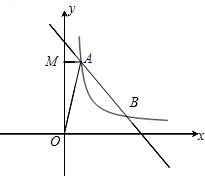 如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数$y=\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com