
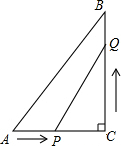
 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=15cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.分析 (1)由于点P从A出发沿AC向C点以1厘米/秒的速度匀速移动,点Q从C出发沿CB向B点以2厘米/秒,而t=4,由此可以用t表示AP、PC、CQ的长度,然后利用勾股定理即可求出PQ的长度;
(2)首先用t分别表示CP,CQ的长度,然后利用三角形的面积公式即可列出关于t的方程,解方程即可解决问题;
解答 解:(1)当t=4时,
∵点P从A出发沿AC向C点以1厘米/秒的速度匀速移动,点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动,
∴AP=4cm,PC=AC-AP=6cm、CQ=2×4=8cm,
∴PQ=$\sqrt{P{C}^{2}+C{Q}^{2}}$=10cm;
(2)∵AP=t,PC=AC-AP=10-t、CQ=2t,
∴S△PQC=$\frac{1}{2}$PC×CQ=t(10-t)=16,
∴t1=2,t2=8,
当t=8时,CQ=2t=16>15,∴舍去,
∴当t=2时,△PQC的面积等于16cm2;
点评 此题考查了勾股定理、三角形的面积公式、相似三角形的性质与判定等知识,综合性很强,比较难,内容比较多,也是一个动点问题,对于学生的能力要求比较高.


科目:初中数学 来源: 题型:解答题
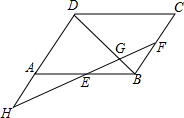 如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG.
如图所示,在?ABCD中,E为AB中点,在BC上取一点F,使BF:FC=1:2,连接EF交DA的延长线于H,交BD于G.试说明:BD=5BG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?
如图,沿AC方向开山修路,为了加快施工进度,要在山的另一面同时施工,工人师傅在AC上取一点B,在小山外取一点D,连接BD并延长,使DF=BD,过F点作AE的平行线FM,交ED的延长线于点M,测量FM的长就是BE的长,你知道其中的道理吗?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查春节联欢晚会在武汉市的收视率 | |
| B. | 了解全班同学参加社会实践活动的情况 | |
| C. | 调查某品牌食品的色素含量是否达标 | |
| D. | 了解一批手机电池的使用寿命 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com