
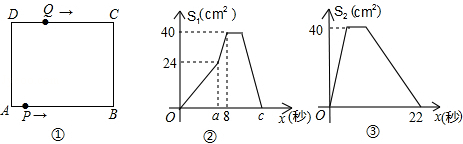
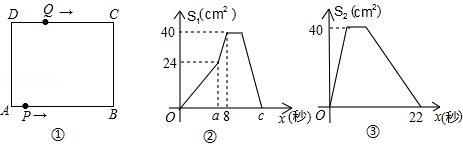
��ͼ�٣��ھ���ABCD�У�AB=10cm��BC=8cm����P��A��������A��B��C��D·���˶�����Dֹͣ����Q��D��������D��C��B��A·���˶�����Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1cm����Q���ٶ�Ϊÿ��2cm��a��ʱ��P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��bcm����Q���ٶȱ�Ϊÿ��dcm��ͼ���ǵ�P����x����APD�����S1��cm2����x���룩�ĺ�����ϵͼ��ͼ���ǵ�Q����x����AQD�����S2��cm2����x���룩�ĺ�����ϵͼ��
��1������ͼ�ڣ���a��b��ͼ���е�cֵ��
��2����d��ֵ��
��3�����P�뿪��A��·��Ϊy1��cm������Q����A�����ߵ�·��Ϊy2��cm������ֱ�д������P��Q�ı��ٶȺ�y1��y2���������˶�ʱ��x���룩�ĺ�����ϵʽ�������P��Q����ʱx��ֵ��
��4������Q������_________����ʱ����P����Q���˶�·��������·��Ϊ25cm��
��
�⣺��1���۲�ͼ�ڵ�S��APD=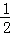 PA•AD=
PA•AD= ��a��8=24��
��a��8=24��
��a=6���룩��
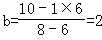 ������/�룩��
������/�룩��
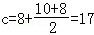 ���룩��
���룩��
��2��������ã�
��22��6��d=28��12��
���d=1������/�룩��
��3����a=6��b=2������P��Q�ı��ٶȺ�y1��y2���������˶�ʱ��x���룩�ĺ�����ϵʽΪ��
y1=6+2��x��6��=2x��6��
y2=28��[12+1����x��6��]=22��x��
�������2x��6=22��x��
��x=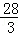 ���룩��
���룩��
��4������Q����17��ʱ����P�����Dֹͣ�˶�����Q�����˶�2�룬
�����˶�19��ʱ����ʹP��Q���������˶�·��������·��Ϊ25cm��
��Q����1s�����P��Q���25cm�����Q����x�룬��P����Q���25cm��
��2x+x=28��25��
���x=1��
�൱��Q����1��19��ʱ����P����Q���˶�·��������·��Ϊ25cm��
�ʴ�Ϊ��1��19��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����ÿ�����ֱ�������ľ���ij��ȣ������Dz��ܰڳ������ε��ǣ�������
| �� | A�� | 4cm��5cm��6cm | B�� | 3cm��3cm��3cm | C�� | 3cm��4cm��5cm | D�� | 1cm��2cm��3cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij��Ʒ�Ľ���Ϊ1000Ԫ���ۼ�Ϊ2000Ԫ����������״�����ã��̵�������۳��ۣ�����Ҫ��֤������20%�����̵�������_________���ۣ�
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
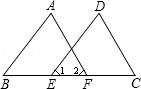
��ͼ����֪��A=��D����1=��2��BE=CF��B��E��F��C��һ��ֱ���ϣ�
��֤����ABF�ա�DCE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ���ڴ�����4����ȫ��ͬ��С�����Ƿֱ���Ϊ�٣��ڣ��ۣ��ܣ����������һ��С��¼��Żأ����������һ��С��������������С��ı����ͬ�ĸ����ǣ�������
| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڡ�ABC�У�AB=AC����A=40�㣬��D��AC�ϣ�BD=BC�����ABD�Ķ����������㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ijƷ��ţ�̹�Ӧ���ṩ��A��B��C��D��E���ֲ�ͬ ��ζ��ţ�̹�ѧ�����ã�ϴ����ѧΪ���˽�ѧ���Բ�ͬ��ζ��ţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨ÿ�в�ͬ��ζ��ţ�̵��������ͬ������������������������������ͳ��ͼ��
��ζ��ţ�̹�ѧ�����ã�ϴ����ѧΪ���˽�ѧ���Բ�ͬ��ζ��ţ�̵�ϲ�ã���ȫУ����ţ�̵�ѧ��������������飨ÿ�в�ͬ��ζ��ţ�̵��������ͬ������������������������������ͳ��ͼ��
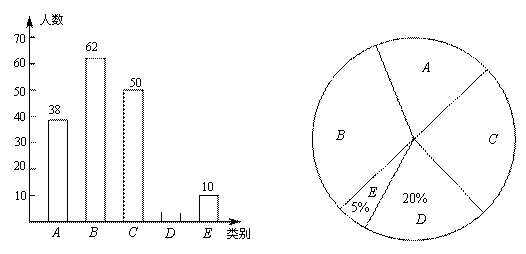
��1�����α������ѧ���� ����
��2����ȫ���������ͳ��ͼ���������ϲ��C��ζ��ţ�̵�ѧ������������ͳ��ͼ�е�Բ�ĽǵĶ�����
��3����У����1200��ѧ�������˸�Ʒ�Ƶ�ţ�̣�ţ�̹�Ӧ��ÿ��ֻΪÿ����ţ�̵�ѧ������һ��ţ�̣�Ҫʹѧ��ÿ�춼�ܺȵ��Լ�ϲ�õĿ�ζ��ţ�̣�ţ�̹�Ӧ��ÿ��������У��ţ���У�B��ζţ��Ҫ��C��ζţ�̶��Ͷ��ٺУ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com