【答案】
分析:由平移的性质求得点A、B的坐标,不难得出∠POM=∠AOB=∠ABO=∠ACD,如果△ACD是等腰三角形,可分三种情况:
①AC=AD,∠ACD=∠ADC,已证得∠AOB=∠ABO=∠ACD=∠ADC,此时C、D与O、B重合,C点坐标即为原点坐标.
②CA=CD,如图11,∠AOC=∠ABO+∠OAB,∠CBD=∠AOB+∠OAB,因此∠AOC=∠OBD,不难得出△AOC≌△CBD,那么OA=BC,可在直角三角形AOH中,求出OA的长,即可得出BC的值,进而可求出C点坐标.
③DA=DC,此时∠DAC=∠ACD,而上面证得∠ACD=∠ABO=∠POM,那么∠CAB=∠ABC,即CA=CB,可设出C点坐标,然后表示出BC、AC、CH的长,在直角三角形ACH中,根据勾股定理即可求出C的坐标.
解答:
解:△ACD能为等腰三角形.
由平移的性质可得,A点坐标
为(m,m
2),B点坐标为(2m,0).
设C点坐标为(x,0),过A点作AH⊥x轴,垂足为H,连接AO,∵A点坐标为(m,m
2),
∴H点坐标为(m,0),AH=m
2.
∵B点坐标为(2m,0),
∴OH=BH=m.∴AB=AO,
∴∠ABC=∠AOB,由已知可得,AB∥OP,
∴∠ABC=∠POM.
又∵∠ACD=∠POM,
∴∠ACD=∠ABC=∠AOB.
若△ACD为等腰三角形,则AC=AD,或CD=CA,或DA=DC.
当AC=AD时
如图10,∵AC=AD,
∴∠ACD=∠ADC.
∴∠ADC=∠ACD=∠ABC,
∴点D与点B重合,点C与点O重合,∴C点坐标为(0,0).
当CD=CA时,
方法一:
如图,∵CD=CA,
∴∠CAD=∠CDA.
∵∠ABC=∠AOB,
∴∠CBD=∠AOC.
∵∠ACD=∠ABC,
又∵∠ABC=∠BCD+∠ADC,∠ACD=∠BCD+∠ACB,
∴∠ADC=∠ACB,
∴△BCD≌△OAC,∴BC=OA.
在Rt△AOB中,OA
2=OH
2+AH
2=m
2+(m
2)
2,
∴BC=OA=m
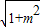
.
∴OC=BC-OB=m

-2m,
∴C点坐标为(2m-m
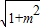
,0).
方法二:
如图11,∵CA=CD,∴∠CAD=∠CDA.
又∵∠ACD=∠ABC,∠CAB=∠DAC,
∴△ACB∽△ADC,∴∠ACB=∠CDA,
∴∠CAD=∠ACB,∴BC=AB.∴BC=OA.
余下部分同方法一.
当DA=DC时,
如图12,∵DA=DC,
∴∠DAC=∠ACD.
∵∠ACD=∠ABC,
∴∠DAC=∠ABC,
∴AC=BC.
∵BC=2m-x,
∴AC=2m-x.
在Rt△ACH中,AC
2=AH
2+CH
2.
∴(2m-x)
2=(m
2)
2+(m-x)
2.
∴x=
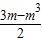
.
∴C点坐标为(
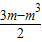
,0).
探索过程一:
由已知可得:AB∥OP,
∴∠ABC=∠POM.
∵∠ACD=∠POM,
∴∠ACD=∠POM=∠ABC.
探索过程二:
若△ACD为等腰三角形,则有三种可能,即AC=AD,或CD=CA,或DA=DC.
当AC=AD时,
∴∠ACD=∠ADC.
选择条件①
当m=1时,P点坐标为(-1,1),由平移性质可得,A点坐标为(1,1),B点坐标为(2,0).
过A点作AH⊥x轴,垂足为H,连接AO,
∴H点坐标为(1,0),AH=1,OH=BH=1.
∴AB=AO,∴∠ABC=∠AOB=45°,∠OAB=90度.
由已知可得,OP∥AB,
∴∠ABC=∠POM.
又∵∠ACD=∠POM,
∴∠ACD=∠ABC=∠AOB=45度.
若△ACD为等腰三角形,则有三种可能,即AC=AD,或CD=CA,或DA=DC.
当AC=AD时,
如图13,
∵AC=AD,
∴∠ACD=∠ADC.
∵∠ACD=∠ABC,
∴∠ABC=∠ADC=∠AOB,
∴点D与点B重合,点C与点O重合,
∴C点坐标为(0,0).
当CA=CD时,
方法一:
如图14,
∵CA=CD,
∴∠CAD=∠CDA.
∵∠ACB=∠AOB+∠OAC,
∴∠ACD+∠DCB=∠AOB+∠OAC,
∴∠DCB=∠OAC.
又∵∠AOB=∠ABC,
∴△BCD≌△OAC,
∴BC=OA.
在∵DA=DC中,OB
2=OA
2+AB
2=2OA
2,
∴4=2OA
2,
∴OA=
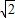
.∴OC=OB-BC=OB-OA=2-
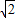
,
∴C点坐标为(2-
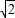
,0).
方法二:
如图14,∵CA=CD,
∴∠CAD=∠CDA.
又∵∠ACD=∠ABC,∠CAD=∠BAC,
∴△ACD∽△ABC,
∴∠CDA=∠ACB.
∴∠CAD=∠ACB,
∴AB=BC.
在Rt△ACH中,OB
2=OA
2+AB
2=2AB
2,
∴4=2AB
2,
∴AB=
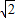
.∴BC=

,
∴OC=OB-BC=2-

,
∴C点坐标为(2-
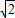
,0).
当DA=DC时,
如图15,∵DA=DC,
∴∠ACD=∠DAC.
∵∠ACD=45°,
∴∠DAC=45°,
∵∠OAB=90°,
∴AC平分∠OAB,
又∵AO=AB,
∴C是OB中点,
∴C点坐标为(1,0).
选择条件②
当m=2时,P点坐标为(-2,4),由平移的性质得,
A点坐标为(2,4),B点坐标为(4,0).
连接OA,过A点作AH⊥x轴,垂足为H,
∴H点坐标为(2,0),AH=4,OH=BH=2,
∴AB=AO,
∴∠ABC=∠AOB.
由已知可得,OP∥AB,
∴∠ABC=∠POM.
又∵∠ACD=∠POM,
∴∠ACD=∠ABC=∠AOB.
若△ACD为等腰三角形,则有三种可能,
即AC=AD,或CD=CA,或DA=DC.
当AC=AD时,
如图16.
∵AC=AD,
∴∠ACD=∠ADC.
又∵∠ACD=∠ABC=∠AOB,
∴∠ACD=∠ABC=∠AOB=∠ADC.
∴点D与点B重合,点C与点O重合,
∴C点坐标为(0,0).(5分)
当CA=CD时,
方法一:
如图17,∵CA=CD,
∴∠CAD=∠CDA.
∵∠ABC=∠ADC+∠BCD,
又∵∠ACD=∠ACB+∠BCD,∠ACD=∠ABC,
∴∠ADC=∠ACB.(6分)
又∵∠ABC=∠AOB,
∴∠CBD=∠AOC,
∴△CBD≌△AOC,
∴BC=OA.(7分)
在Rt△AOH中,OA
2=AH
2+OH
2=4
2+2
2=20,
∴BC=OA=2
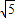
.∵OC=BC-OB=2
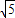
-4,
∴C点坐标为(4-2
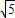
,0).
方法二:
如图17,∵CA=CD,
∴∠CAD=∠CDA.
∵∠ACD=∠ABC,
又∵∠CAD=∠BAC,
∴△ACD∽△ABC,
∴∠CDA=∠ACB,
∴∠CAD=∠ACB.
∴AB=BC.
在Rt△ABH中,AB
2=AH
2+BH
2=4
2+2
2=20,
∴BC=AB=2
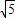
.∴OC=BC-OB=2
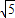
-4.
∴C点坐标为(4-2
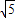
,0).
当DA=DC时,
如图18,∵DA=DC,
∴∠DAC=∠ACD.
∵∠ACD=∠ABC,
∴∠DAC=∠ABC.
∴AC=BC.
在Rt△ACH中,AC
2=AH
2+CH
2,
∴(4-x)
2=4
2+(2-x)
2,
∴x=-1.∴C点坐标为(-1,0).
点评:本题主要考查了抛物线的性质和二次函数图象的平移、等腰三角形的判定和性质、相似三角形的判定和性质等知识,本题在不确定等腰三角形的腰和底的情况下要分类讨论,以免漏解.本题综合性强,难度较高.



 .
. -2m,
-2m,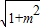 ,0).
,0).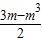 .
.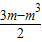 ,0).
,0).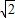 .∴OC=OB-BC=OB-OA=2-
.∴OC=OB-BC=OB-OA=2-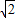 ,
,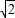 ,0).
,0).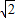 .∴BC=
.∴BC= ,
, ,
,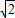 ,0).
,0).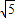 .∵OC=BC-OB=2
.∵OC=BC-OB=2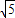 -4,
-4,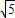 ,0).
,0).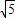 .∴OC=BC-OB=2
.∴OC=BC-OB=2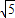 -4.
-4.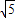 ,0).
,0).

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2