
已知,如图,已知AD、AE分别是△ABC的中线,高线,且AB=5cm,AC=3cm;则△ABD和△ADC的周长之差等于 cm;△ABD与△ACD的面积关系是 .

2,相等
【解析】
试题分析:根据△ABD的周长=AB+AD+BD,△ACD的周长=AC+AD+CD,AD是BC的中线,可得△ABD与△ACD的周长的差=AB-AC,三角形的中线把三角形分成面积相等的两个三角形,据此答题即可.
△ABD的周长=AB+AD+BD,△ACD的周长=AC+AD+CD,
∵AD是BC的中线,
∴BD=CD,
∵AB=5cm,AC=3cm,
∴△ABD的周长-△ACD的周长=AB+AD+BD-AC-AD-CD=AB-AC=2(cm),
∵△ABD与△ACD的底相等,高都是AE,
∴它们的面积相等.
考点:本题考查了三角形的中线概念和性质
点评:解答本题的关键是熟练掌握三角形的中线把三角形分成面积相等的两个三角形.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.
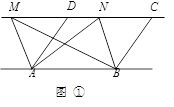
求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
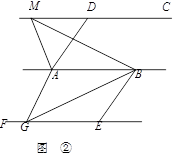
(2)结论应用:
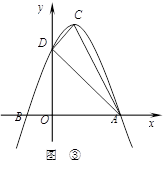
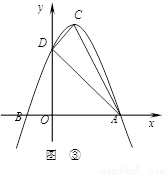
如图③,抛物线的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚
查看答案和解析>>
科目:初中数学 来源: 题型:
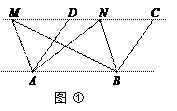

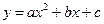 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线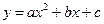 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由. 
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:解答题
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.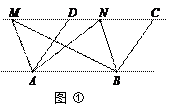
求证:△ABM与△ABN的面积相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由. 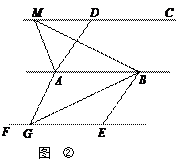
(2)结论应用:
如图③,抛物线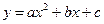 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线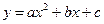 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等? 若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚ 
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁丹东) 题型:解答题
(1)探究新知:
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.
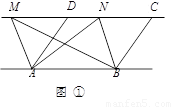
求证:△ABM与△ABN的面积相等.
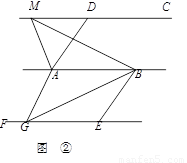
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
如图③,抛物线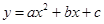 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线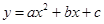 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?
若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?
若存在,请求出此时点E的坐标,若不存在,请说明理由.
﹙友情提示:解答本问题过程中,可以直接使用“探究新知”中的结论.﹚
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com