Question

如图，在直角坐标系中，已知点A（-1，0）、B（0，2），将线段AB绕点A按逆时针方向旋转90°至AC．
（1）点C的坐标为______；
（2）若二次函数y=x²-ax-2的图象经过点C．
①求二次函数y=x²-ax-2的关系式；
②当-1≤x≤4时，直接写出函数值y对应的取值范围；
③在此二次函数的图象上是否存在点P（点C除外），使△ABP是以AB为直角边的等腰直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．

Answer 1

解：（1）过点C作CD⊥x轴于点D，
∵旋转角为90°，
∴∠BAO+∠CAD=180°-90°=90°，
又∵∠BAO+∠ABO=90°，
∴∠CAD=∠ABO，
在△ABO和△CAD中，
∵，
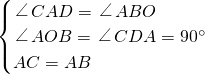
∴△ABO≌△CAD（AAS），
∴AD=BO=2，CD=AO=1，
∴OD=AO+AD=1+2=3，
∴点C的坐标为（-3，1）；

（2）①∵二次函数y=x²-ax-2的图象经过点C（-3，1），
∴×（-3）²-（-3）a-2=1，
解得a=-，
故二次函数的关系式为y=x²+x-2；

②∵y=x²+x-2=（x+）²-，
∴当-1≤x≤4时，x=-时取得最小值y=-，
x=4时，取得最大值y=（4+）²-=8，
所以，函数值y的取值范围为：-≤y≤8；

③（i） 当A为直角顶点时，延长CA至点P₁，使AP₁=AC=AB，则△ABP₁是以AB为直角边的等腰直角三角形，过点P₁作P₁E⊥x轴，
∵AP₁=AC，∠EAP₁=∠DAC，∠P₁EA=∠CDA=90°，
∴△EP₁A≌△DCA，
∴AE=AD=2，EP₁=CD=1，
∴可求得P₁的坐标为（1，-1），
经检验点P₁在二次函数的图象上；
（ii） 当B点为直角顶点时，过点B作直线L⊥BA，在直线L上分别取BP₂=BP₃=AB，得到以AB为直角边的等腰直角△ABP₂和等腰直角△ABP₃，
作P₂F⊥y轴，同理可证△BP₂F≌△ABO，
则P₂F=BO=2，BF=OA=1，
可得点P₂的坐标为（2，1），
经检验P₂点在二次函数的图象上，
同理可得点P₃的坐标为（-2，3），
经检验P₃点不在二次函数的图象上．
综上所述：二次函数的图象上存在点P₁（1，-1），P₂（2，1）两点，使得△ABP₁和△ABP₂是以AB为直角边的等腰直角三角形．
分析：（1）过点C作CD⊥x轴于点D，然后利用“角角边”证明△ABO和△CAD全等，根据全等三角形对应边相等可得AD=BO，CD=AO，然后求出OD，再根据点C在第二象限，写出点C坐标即可；
（2）①把点C的坐标代入二次函数解析式求出a的值即可得解；
②把二次函数解析式整理成顶点式形式，然后根据二次函数的增减性求出最大值与最小值，即可得到函数值y的取值范围；
③分点A是直角顶点时求出点P的坐标，点B是直角顶点时求出点P的坐标，然后验证是否在二次函数图象上即可．
点评：本题是二次函数综合题型，主要考查了旋转变换的旋转，全等三角形的判定与性质，待定系数法求二次函数解析式，二次函数的最值问题，二次函数的增减性以及等腰直角三角形的性质，二次函数图象上点的坐标特征，综合性较强，但难度不是很大，要注意分情况讨论．