
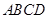 中,
中,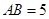 ,
,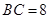 ,
,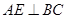 ,垂足为
,垂足为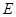 ,
,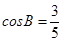 .
.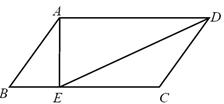
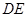 的长;
的长;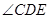 的正弦值.
的正弦值.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 ≈1.414,
≈1.414, 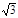 ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
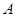 处观测到河对岸水边有一点
处观测到河对岸水边有一点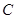 ,测得
,测得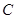 在
在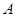 北偏西
北偏西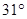 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达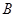 处,测得
处,测得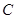 在
在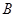 北偏西
北偏西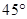 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈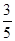 ,sin31°≈
,sin31°≈ )
) 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com