
 如图,已知等边△ABC中,M,N是BC所在直线上的点,∠MAN=120°,求证:BC2=BM•CN.
如图,已知等边△ABC中,M,N是BC所在直线上的点,∠MAN=120°,求证:BC2=BM•CN.  开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:解答题
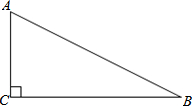 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 生活用水量 | 工业用水量 | 农业用水量 | 生态用水量 |
| 2008 | 729.3 | 1397.1 | 3663.5 | 120.2 |
| 2009 | 748.2 | 1390.9 | 3723.1 | 103.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
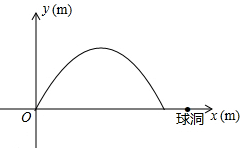 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{16}{5}$x,其中y(m)是球的飞行速度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有4m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
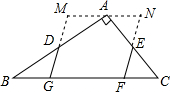 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D、E分别是AB、AC的中点,点G、F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是$\frac{49}{5}$≤l<13..
如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D、E分别是AB、AC的中点,点G、F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是$\frac{49}{5}$≤l<13..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com