
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.

【答案】(1)证明见解析;(2)65°
【解析】试题分析:⑴由AB=AC,可知∠B=∠ C,根据题意易得△ BDE ≌ △ CEF(SAS),从而得到DE=EF,命题得证.
⑵因为∠ A=50°,所以∠ B=∠ C=65°,由⑴可知,∠BDE=∠CEF,所以∠DEB+∠CEF=
∠DEB+∠ BDE=115°,从而∠ DEF=180°-115°=65°.
试题解析:⑴∵ AB=AC,∴ ∠B=∠ C.
在△ BDE和△ CEF中,
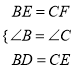 ,
,
∴ △ BDE ≌ △ CEF(SAS),则DE=EF,故△ DEF是等腰三角形.
⑵在△ABC中,∵∠A=50°,∴∠B=∠C=65°.
∵ △ BDE ≌ △ CEF,∴ ∠BDE=∠CEF,
∴ ∠DEB+∠CEF=∠DEB+∠ BDE=180°-65°=115°,
则 ∠ DEF=180°-(∠DEB+∠CEF)=180°-115°=65°.


科目:初中数学 来源: 题型:
【题目】在检测一批刚出厂的足球的质量时,随机抽取了4个足球来测量其质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检测结果如下表:
足球的编号 | 1 | 2 | 3 | 4 |
与标准质量的差(克) | +3 | +2 | ﹣1 | ﹣2 |
则生产较合格的足球的编号是( )
A.1号B.2号C.3号D.4号
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有_____个白球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备购进A、B两种品牌台灯,其中A每盏进价比B进价贵30元,A售价120元,B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.
(1)求A、B的进价;
(2)超市打算购进A、B台灯共100盏,要求A、B的总利润不得少于3400元,不得多于3550元,问有多少种进货方案?
(3)在(2)的条件下,该超市决定对A进行降价促销,A台灯每盏降价m(8<m<15)元,B不变,超市如何进货获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习“有理数加法“时,我们利用“(+5)+(+3)=+8,(-5)+(-3)=-8,……”抽象归纳推出了“同号两数相加,取相同的符号,并把绝对值相加”的加法法则.这种推导方法叫( )
A.排除法B.归纳法C.类比法D.数形结合法
查看答案和解析>>
科目:初中数学 来源: 题型:
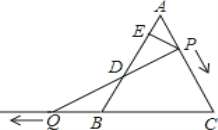
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com