
���� ��1����������У���15�ı������У�15��30��45��������15���У�1��3��5��15��Ϊ�˲��ظ�������15ֻ��һ�Σ���ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2������kȡ��ֵ�����ܱ�1�����������Ϊ1��ѧ�������еĸ���Ϊ1����100%���������Գ鵽�������ѧ�����ʲ�Ϊ100%����֪����Ϸ����ƽ��
��3�������Ϊ���ȳ��һ�ţ��������֣�Ȼ��ÿ�����ּ�5���õ���ţ������ּ�5����50�������50����Ϊ��ţ�ֱ���õ�10��Ϊֹ��
��� �⣺��1����������У���15�ı������У�15��30��45��������15���У�1��3��5��15��Ϊ�˲��ظ�������15ֻ��һ�Σ���
����15��������������15������6����
��ȡ���Ŀ�Ƭ�������15�ı�����������15�ĸ���Ϊ��$\frac{6}{50}$=$\frac{3}{25}$��
��2������ƽ��
������kȡ��ֵ�����ܱ�1�����������Ϊ1��ѧ�������еĸ���Ϊ1����100%��
�������Գ鵽�������ѧ�����ʲ�Ϊ100%��
���ƽ��
��3���ȳ��һ�ţ��������֣�Ȼ��ÿ�����ּ�5���õ���ţ������ּ�5����50�������50����Ϊ��ţ�ֱ���õ�10��Ϊֹ��
��ÿ���˶��л��ᣩ
���� ���⿼�������Ϸ��ƽ�Ե��жϣ��ж���Ϸ��ƽ�Ծ�Ҫ����ÿ���¼��ĸ��ʣ�������Ⱦ�ƽ������Ͳ���ƽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
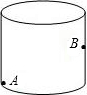 ��һԲ����ʳƷ�У����ĸߵ���8cm������ֱ��Ϊ$\frac{18}{��}$cm���������е��ٶ�Ϊ2cm/s������ں����µ����A����һֻ���ϣ�����Ե����ڶ����в���B����ʳ���ô��������Ҫ����ʱ�䣿���еĺ�Ⱥ����ϵĴ�С���Բ��ƣ�����ɺ����ţ�
��һԲ����ʳƷ�У����ĸߵ���8cm������ֱ��Ϊ$\frac{18}{��}$cm���������е��ٶ�Ϊ2cm/s������ں����µ����A����һֻ���ϣ�����Ե����ڶ����в���B����ʳ���ô��������Ҫ����ʱ�䣿���еĺ�Ⱥ����ϵĴ�С���Բ��ƣ�����ɺ����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ʮ��λ�� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | �� |
| ����� | 0 | 1 | 10 | 11 | 100 | 101 | 110 | �� |
| A�� | 84 | B�� | 85 | C�� | 170 | D�� | 171 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=$\frac{\sqrt{5}��\sqrt{11}}{2}$ | B�� | x=$\frac{\sqrt{5}��\sqrt{29}}{4}$ | C�� | x=$\frac{-\sqrt{5}��\sqrt{29}}{2}$ | D�� | x=$\frac{-\sqrt{5}��\sqrt{29}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y3��y2��y1 | B�� | y3��y1��y2 | C�� | y2��y1��y3 | D�� | y1��y2��y3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ���ǵIJ���һ����������� | B�� | ��ǵIJ���һ���Ƕ۽� | ||
| C�� | ֱ�ǵIJ��ǿ�������ǻ�۽� | D�� | ��ǺͶ۽ǻ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2•x3=x6 | B�� | ��xn+1��2=x2n+1 | C�� | ��-2xy2��2=4x2y4 | D�� | 2x+x=2x2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com