
分析 (1)根据积的乘方和同底数幂的乘法可以解答本题;
(2)根据完全平方公式和平方差公式可以解答本题;
(3)先化简题目中的式子,再将a的值代入即可解答本题.
解答 解:(1)(-2a2)2•a4-(-5a4)2
=4a4•a4-25a8
=4a8-25a8
=-21a8;
(2)4(a-b)2-(2a+b)(-b+2a)
=4a2-8ab+4b2-4a2+b2
=-8ab+5b2;
(3)(3a+2)•(3a-2)-8a•(a-1)-(a-1)2
=9a2-4-8a2+8a-a2+2a-1
=10a-5,
当a=-$\frac{1}{5}$时,原式=10×(-$\frac{1}{5}$)-5=-2-5=-7.
点评 本题考查整式的混合运算-化简求值,解答本题的关键是明确整式的化简求值的方法.


科目:初中数学 来源: 题型:解答题
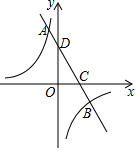 已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.
已知直线y=mx+4与反比例函数y=$\frac{k}{x}$(k<0)的图象交于A,B两点,与x轴,y轴分别交于点C,D,OD=2OC,点A的纵坐标为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
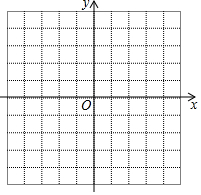 如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com