
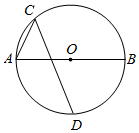
 如图.AB是⊙O的直径,∠BAC=60°,D为半圆的中点,若⊙O的半径为4,求CD的长.
如图.AB是⊙O的直径,∠BAC=60°,D为半圆的中点,若⊙O的半径为4,求CD的长. 分析 作辅助线,构建直角三角形,利用D为半圆的中点得等腰直角三角形AOD,求出AD的长,根据等腰三角形的性质得:∠ADE=30°,所以利用30°角所对的直角边是斜边的一半求AE的长,利用勾股定理求出DE的长,证明△ACE是等腰直角三角形,求出CE的长,相加即可得CD的长.
解答  解:连接AD、OD、OC,过A作AE⊥CD于E,
解:连接AD、OD、OC,过A作AE⊥CD于E,
∵D为半圆的中点,AB为⊙O的直径,
∴∠AOD=90°,
∵AO=OD=4,
∴AD=4$\sqrt{2}$,∠ADO=45°,
∵OC=OA,∠BAC=60°,
∴△ACO是等边三角形,
∴AC=AO=4,∠AOC=60°,
∴∠COD=60°+90°=150°,
∵OC=OD,
∴∠OCD=∠ODC=15°,
∴∠ADC=∠ADO-∠ODC=45°-15°=30°,
在Rt△AED中,AE=$\frac{1}{2}$AD=$\frac{1}{2}$×$4\sqrt{2}$=2$\sqrt{2}$,
由勾股定理得:DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(2\sqrt{2})^{2}}$=2$\sqrt{6}$,
∵∠ACO=60°,∠OCD=15°,
∴∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=$\frac{AC}{\sqrt{2}}$=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,
∴CD=CE+ED=2$\sqrt{2}$+2$\sqrt{6}$.
点评 本题考查了圆周角定理、等腰三角形、等边三角形的性质和判定,根据等腰三角形中等边对等角和等边三角形的性质求出特殊角的度数,利用勾股定理求边的长度.


科目:初中数学 来源: 题型:解答题
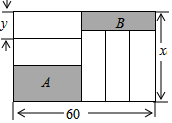 如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).
如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A,B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB,根据下列语句画出图形计算:
如图,已知线段AB,根据下列语句画出图形计算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
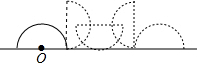 一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)
一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
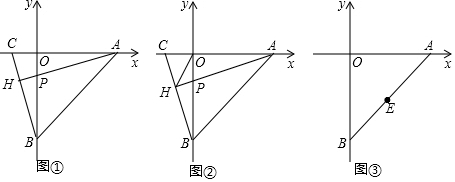
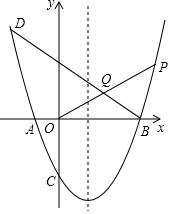 如图,已知抛物线y=ax2+bx+c过点D(-2,5),与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-3).
如图,已知抛物线y=ax2+bx+c过点D(-2,5),与x轴交于点A(-1,0)和点B,与y轴交于点C(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 20或24 | D. | 24或26 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )
已知a,b,c在数轴上的位置如图所示,则下列结论正确的是( )| A. | b表示负数,a,c表示正数,且|a|>|b| | B. | b表示负数,a,c表示正数,且|b|<|c| | ||
| C. | b表示负数,a,c表示正数,且|c|<|b| | D. | b表示负数,a,c表示正数,且|-a|>|b| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com