
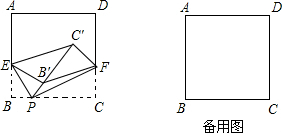
 =60°,沿PE翻折△EBP得到△EB′P.F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点C′落在射线PB′上.
=60°,沿PE翻折△EBP得到△EB′P.F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点C′落在射线PB′上. ,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°,
,C'P=CP=BC-BP=3,∠C'PF=∠CPF=30°, ,C'B'=C'P-B'P=3-1=2,
,C'B'=C'P-B'P=3-1=2, B'E×B'C'+
B'E×B'C'+ C'F×B'C'=
C'F×B'C'= +
+ =2
=2 ;
; m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°,
m,C'P=CP=BC-BP=4-m,∠C'PF=∠CPF=30°, (4-m),C'B'=C'P-B'P=4-m-m=4-2m,
(4-m),C'B'=C'P-B'P=4-m-m=4-2m, B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C' ×
× m×(4-2m)+
m×(4-2m)+ ×
× (4-m)×(4-2m)
(4-m)×(4-2m) m2+2
m2+2 m+
m+ m2-2
m2-2 m+
m+
 m2+
m2+ (0<m<2).
(0<m<2). 时,
时,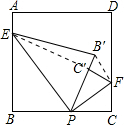
 m,B'C'=m-(4-m)=2m-4,FC'=
m,B'C'=m-(4-m)=2m-4,FC'= (4-m),
(4-m), B'E×B'C'+
B'E×B'C'+ C'F×B'C'
C'F×B'C' ×
× m×(2m-4)+
m×(2m-4)+ ×(2m-4)×
×(2m-4)× (4-m)
(4-m) m2-2
m2-2 m+(m-2)×(
m+(m-2)×( -
- m)
m) m2-2
m2-2 m+
m+ m-
m- m2-
m2- +
+ m
m m2-
m2- (2<m≤
(2<m≤ ).
). ;-
;- m2+
m2+ (0<m<2),
(0<m<2), m2-
m2- (2<m≤
(2<m≤ ).
). ,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.
,CP=C'P=4-1=3,也可得出C'F,继而根据S四边形EB′FC′=S△EB'C'+S△B'C'F可得出答案.

科目:初中数学 来源: 题型:
 附加题
附加题| 3 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
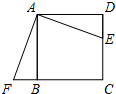 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com