练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．下列各组数中，以它们为边长的线段不能构成直角三角形的是（　　）
    A．1，$\sqrt{2}$，$\sqrt{3}$B．3，4，5C．5，12，13D．2，2，3

    分析 欲求证是否为直角三角形，利用勾股定理的逆定理即可．这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．

    解答 解：A、12+（$\sqrt{2}$）2=3=（$\sqrt{3}$）2，故是直角三角形，故错误；
    B、42+32=25=52，故是直角三角形，故错误；
    C、52+122=169=132，故是直角三角形，故错误；
    D、22+22=8≠32，故不是直角三角形，故正确．
    故选D．

    点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．下列调查中，适宜采用全面调查方式的是（　　）
    A．调查某品牌钢笔的使用寿命
    B．了解某市学生的视力情况
    C．调查乘坐飞机的乘客是否携带违禁物品
    D．了解某市学生课外阅读情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

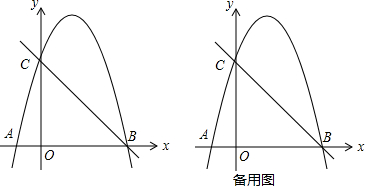    19．如图，已知抛物线y=ax2-3ax-4a（a≠0）与x轴交于A、B两点（A在B的左侧），与y轴交于点C，∠ACB=90°，点D 的坐标为（0，3）
    （1）求A、B、C的坐标及a的值；
    （2）直线l经过点D，与抛物线交于M、N，若MN2=DM•DN，求直线l的解析式；
    （3）过点D 作直线DH⊥OD，P为直线DH上的一动点．是否存在点P，使sin∠OPB的值最大？若存在，求出此时sin∠OPB的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．一个不透明的口袋中有7个红球，5个黄球，4个绿球，这些球除颜色外没有其它区别，现从中任意摸出一球，如果要使摸到绿球的可能性最大，需要在这个口袋中至少再放入多少个绿球？请简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．点P（-2，3）关于y轴的对称点的坐标是（　　）
    A．（2，3 ）B．（-2，-3）C．（-2，3）D．（-3，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．小颖随机抽样调查本班20名女同学所穿运动鞋尺码，并统计如表：
    尺码/cm21.522.022.523.023.5
    人数24383
    学校附近的商店经理根据表中决定本月多进尺码为23.0cm的女式运动鞋，商店经理的这一决定应用了哪个统计知识（　　）
    A．众数B．中位数C．平均数D．方差

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．△ABC为等腰直角三角形，∠ACB=90°，AC=BC=2，P为线段AB上一动点，D为BC上中点，则PC+PD的最小值为（　　）
    A．$\sqrt{3}$B．3C．$\sqrt{5}$D．$\sqrt{2}+1$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．因式分解：
    （1）-3x3+6x2y-3xy2                                  
    （2）25（a+b）2-9（a-b）2
    （3）15x3y-25x2y2-10xy3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．嘉淇同学解分式方程$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$时，她是这样做的：
    方程两边同时乘以（x-2），得：x-3+1=-3，…第一步
    移项且合并同类项，得：x=-1，…第二步
    检验：把x=-1代入x-2，得：
    x-2=-1-2=-3≠0，…第三步
    所以，x=-1是原分式方程的解…第四步
    （1）嘉淇的解法从第一步开始出现错误，事实上，这个分式方程的解是x=1．
    （2）解分式方程：$\frac{2}{{x}^{2}-1}$+$\frac{x}{1-x}$=-1．

    查看答案和解析>>

    同步练习册答案