把一副普通扑克牌中的4张;黑桃2,红心3,梅花4,黑桃5,洗匀后正面朝下放在桌面上
(1)从中随机抽取一张牌是黑桃的概率是多少?
(2)从中随机抽取一张,再从剩下的牌中随机抽取另一张.请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果,并求抽取的两张牌牌面数字之和大于7的概率.
【答案】
分析:列举出所有情况,看所求的情况占总情况的多少即可.
解答:解:(1)共有4种情况,其中黑桃有2张,从中随机抽取一张牌是黑桃的概率为

;
(2)抽取的两张牌牌面数字所有可能出现的结果,用表格表示如下:
后抽取的牌牌面数字
后抽取的牌牌面数字 | 2 | 3 | 4 | 5 |
| 2 | | (2,3) | (2,4) | (2,5) |
| 3 | (3,2) | | (3,4) | (3,5) |
| 4 | (4,2) | (4,3) | | (4,5) |
| 5 | (5,2) | (5,3) | (5,4) | |
先抽取的牌牌面数字也可树状图表示如下:
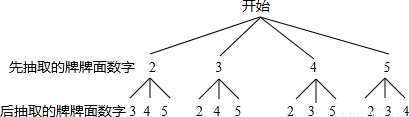
所有可能出现的结果有(2,3),(2,4),(2,5),(3,2),(3,4),(3,5),(4,2),(4,3),(4,5),(5,2),(5,3),(5,4),由表格(或树状图)可以看出,抽取的两张牌可能出现的结果有12种.它们出现的可能性相等,而两张牌牌面数字之和大于7的结果有4种.
所以抽取的两张牌牌面数字之和大于7的概率为

.
点评:本题考查的是用列表法或画树状图法求概率.
列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

 ;
;
 .
.
