
【题目】张大爷要围成一个矩形花圃.花圃的一边利用墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD.设AB边的长为x米.矩形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式及自变量x的取值范围;
(2)当x为何值时,S有最大值?并求出最大值.
(3)当墙的最大可利用长度为10米时,围成花圃的最大面积是多少?

【答案】(1)![]() (2)当AB长为8米时,花圃面积最大为128平方米;
(2)当AB长为8米时,花圃面积最大为128平方米;
(3)当墙的最大可利用长度为10米时,AB=11米时,面积最大为110平方米。
【解析】试题分析: (1)根据题意可以写出S与x之间的函数关系式,并求出x的取值范围;
(2)根据(1)中的函数关系式,可以化为顶点式,从而可以解答本题;
(3)根据二次函数的性质可以解答本题.
试题解析:
(1)由题意可得,
S=x(322x)=2x+32x,
∵![]() ,
,
解得,0<x<16,
即S与x之间的函数关系式是S=2x+32x(0<x<16);
(2)∵S=2x+32x=2(x8)+128,
∴当x=8时,S有最大值,最大值是128平方米;
(3)∵S=2(x8)+128,
由322x≤10得,x≥11,
∴11≤x≤16,
∴当x=11时,S取得最大值,此时S=2(118)+128=110,
即当墙的最大可利用长度为10米时,围成花圃的最大面积是110平方米


科目:初中数学 来源: 题型:
【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在![]() 上的点D处,折痕交OA于点C,则
上的点D处,折痕交OA于点C,则![]() 的长为( )
的长为( )
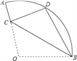
A. 2π B. 3π C. 4π D. 5π
查看答案和解析>>
科目:初中数学 来源: 题型:
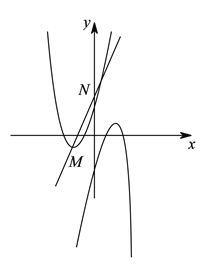
【题目】如图,在平面直角坐标系中,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,先将抛物线
,先将抛物线![]() 沿
沿![]() 轴翻折,再向右平移
轴翻折,再向右平移![]() 个单位长度后得到抛物线
个单位长度后得到抛物线![]() 直线
直线![]() 经过
经过![]() ,
, ![]() 两点.
两点.
(![]() )结合图象,直接写出不等式
)结合图象,直接写出不等式![]() 的解集.
的解集.
(![]() )若抛物线
)若抛物线![]() 的顶点与点
的顶点与点![]() 关于原点对称,求
关于原点对称,求![]() 的值及抛物线
的值及抛物线![]() 的解析式.
的解析式.
(![]() )若直线
)若直线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位长度后,与(
个单位长度后,与(![]() )中的抛物线
)中的抛物线![]() 存在公共点,求代数式
存在公共点,求代数式![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,FE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为![]() ,其中正确的是( )
,其中正确的是( )
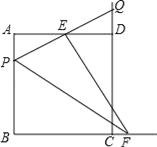
A. ①② B. ①②④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解某个年级的学习情况,在这个年级抽取了50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组] | 50~59分 | 60~69分 | 70~79分 | 80~89分 | 90~99分 |
频率 | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
(1)本次测试90分以上的人数有人;(包括90分)
(2)本次测试这50名学生成绩的及格率是;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好
B.一般
C.不好
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com