
现有一笔直的公路连接M、N两地。甲车从 M 地 驶往 N 地,速度为每小时60km;同时乙车从N地驶往M 地,速度为每小时80 km。途中甲车发生故障,于是停车修理了2.5h,修好后立即开车驶往N地。设乙车行驶的时间为t h,两车之间的距离为S km。已知 S与 t 的函数关系的部分图像如图所示。
(1)求出甲车出发几小时后发生故障。
(2)请指出图中线段 BC 的实际意义;
(3)将S与 t 的函数图像补充完整(需在图中标出相应的数据)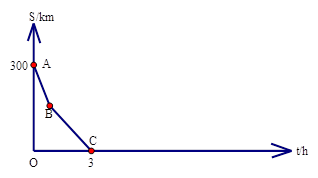
(1)1;(2)乙从1h到3h单独行驶到遇见甲车;(3)补图见解析.
解析试题分析:(1)根据图象,3小时时两车相遇,再求出相遇时甲车行驶的路程,然后根据时间=路程÷速度计算即可得解;
(2)根据甲修车的时间可知BC段只有乙车行驶解答;
(3)分甲修好车前乙单独行驶,甲修好车后至乙车到达M地,甲车到达N地三段分别求出两车间的距离与时间的关系式,然后补全图形即可.
(1)t=3时,两车距离为0,相遇,
∵80×3=240km,
∴发生故障前甲车行驶路程为300-240=60km,
时间=60÷60=1小时;
(2)∵甲停车修理了2.5h,
∴t=3时,甲还在修车,
∴线段BC的实际意义:乙从1h到3h单独行驶到遇见甲车;
(3)甲车再次行驶时,t=1+2.5=3.5h,
乙车到达N地时,t=300÷80=3.75h,
甲车到达M地时,t=300÷60+2.5=7.5h,
所以,3<t≤3.5时,s=80(t-3)=80t-240,
t=3.5时,80t-240=80×3.5-240=40km,
3.5<t≤3.75时,s=80(t-3)+60(t-3.5)=140t-450,
t=3.75时,140t-450=140×3.75-450=75km,
3.75<t≤7.5时,s=60(t-3.75)+75=60t-150,
补全图形如图所示.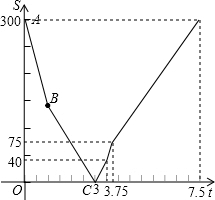
考点:一次函数的应用.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
如图,正方形的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,直线l与直线 y= -2x关于y轴对称,直线l与反比例函数 的图象的一个交点为A(2, m).
的图象的一个交点为A(2, m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知反比例函数 (
(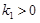 )与一次函数
)与一次函数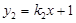 (
(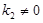 )相交于A、B两点,AC⊥
)相交于A、B两点,AC⊥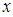 轴于点C.若△OAC的面积为1,且tan∠AOC=2.
轴于点C.若△OAC的面积为1,且tan∠AOC=2.
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当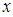 为何值时,反比例函数
为何值时,反比例函数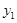 的值大于一次函数
的值大于一次函数 的值?
的值?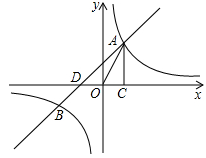
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在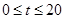 和
和 时,y关于t的函数关系式:
时,y关于t的函数关系式:
当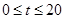 ,y= ;当
,y= ;当 时,y= ;
时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲、乙两人骑车前往A地,他们距A地的路程S(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)、甲、乙两人的速度各是多少?
(2)、求甲距A地的路程S与行驶时间t的函数关系式。
(3)、直接写出在什么时间段内乙比甲距离A 地更近?(用不等式表示)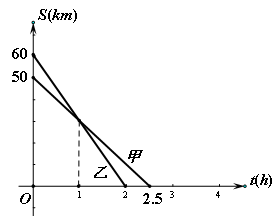
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)若直线MN上存在点P,使得PA+PB的值最小,请直接写出PA的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
书生中学小卖部工作人员到路桥批发部选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量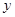 (个)与甲品牌文具盒数量
(个)与甲品牌文具盒数量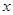 (个)之间的函数关系如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.
(个)之间的函数关系如图所示,当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.
(1)根据图象,求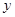 与
与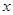 之间的函数关系式;
之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货价;
(3)若小卖部每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学校后勤部决定,准备用不超过6 300元购进甲、乙两种品牌的文具盒,且这两种文具盒全部售出后获利不低于1 795元,问小卖部工作人员有几种进货方案?哪种进货方案能使获利最大?最大获利为多少元?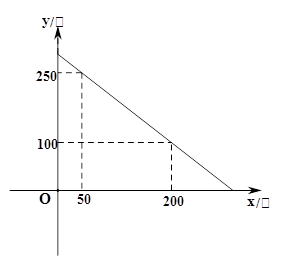
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=-2x+8交x轴于A,交y轴于B i点p在线段AB上,过点P分别向x轴、y轴引垂线,垂足为C、D,设点P的横坐标为m,矩形PCOD的面积为S.
(1)求S与m的函数关系式; (2)当m取何值时矩形PCOD的面积最大,最大值是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com