
分析 先利用因式分解得方法得到原式=$\frac{(a-1)^{2}}{a-1}$+$\frac{\sqrt{(a-1)^{2}}}{a(a-1)}$,再根据a的值化简二次根式,约分后得到原式=a-1-$\frac{1}{a}$,然后把a的值代入计算即可.
解答 解:原式=$\frac{(a-1)^{2}}{a-1}$+$\frac{\sqrt{(a-1)^{2}}}{a(a-1)}$
=a-1+$\frac{|a-1|}{a(a-1)}$,
∵a=$\frac{1}{3+2\sqrt{2}}$<1,
∴原式=a-1+$\frac{-(a-1)}{a(a-1)}$
=a-1-$\frac{1}{a}$
=$\frac{1}{3+2\sqrt{2}}$-1-(3+2$\sqrt{2}$)
=3-2$\sqrt{2}$-1-3-2$\sqrt{2}$
=-1-4$\sqrt{2}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.注意$\sqrt{{a}^{2}}$=|a|.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
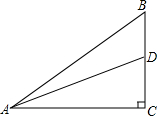 如图,在Rt△ABC中,AB=15,Sin∠BAC=$\frac{3}{5}$,点D是BC边上一点,且BD=4,求:(1)线段AC的长;(2)tan∠ADC的值.
如图,在Rt△ABC中,AB=15,Sin∠BAC=$\frac{3}{5}$,点D是BC边上一点,且BD=4,求:(1)线段AC的长;(2)tan∠ADC的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
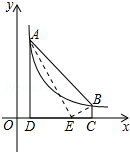 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为(5,0).
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.线段DC上有一点E,当△ABE的面积等于5时,点E的坐标为(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?
冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com