
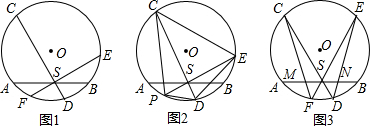
分析 (Ⅰ)先由垂径定理和勾股定理求出OS=1,过点O作CD,EF的垂线,得出矩形,由勾股定理求出OH2,OG2,进而用OG2+OH2=1,建立方程即可得出函数关系式,即极值;
(Ⅱ)先判断出△ESD∽△CSF,进而判断出O,S,N,L四点共圆,同理:O,T,M,S四点共圆,再用相交弦定理即可.
解答 解:(Ⅰ)如图1,
连接OS,OB,
∵点S是AB中点,点O是圆心,
∴OS⊥AB,
AS=$\frac{1}{2}$AB=1,
在Rt△OBS中,OB=2,
∴OS=1,
作OG⊥CD于G,OH⊥EF于H,
∵CD⊥EF,
∴四边形OGSH是矩形,
∴GS=OH,
根据勾股定理得,OG2+GS2=OS2=1,
∴OG2+OH2=1
连接OC,
∴OG2=OC2-CD2=4-($\frac{x}{2}$)2
同理:OH2=4-($\frac{y}{2}$)2,
∴4-($\frac{x}{2}$)2+4-($\frac{y}{2}$)2=1,
∴y=$\sqrt{28-{x}^{2}}$(2$\sqrt{3}$≤x≤4)
∵CD⊥EF,
∴S=S四边形CEDF=$\frac{1}{2}$xy,
∴S2=$\frac{1}{4}$x2×y2=$\frac{1}{4}$x2(28-x2)=-$\frac{1}{4}$(x2-14)2+49,
∴当x2=14即x=$\sqrt{14}$时,S最大=7,
(Ⅱ)如图3,
过O作OL⊥ED,OT⊥CF.连接ON,OM,OS,SL,ST,
∴LE=$\frac{1}{2}$ED,CT=$\frac{1}{2}$FC
∵∠ESD=∠CSF,∠SED=∠SCF,
∴△ESD∽△CSF,
∴$\frac{ES}{CS}=\frac{ED}{FC}$,
∴$\frac{ES}{CS}=\frac{LE}{CT}$
∵∠E=∠C,
∴△ESL∽△CST,
∴∠SLN=∠STM.
∵S是AB中点,
∴OS⊥AB.
∴∠OSN=∠OLN=90°,
∴∠OSN+∠OLN=180°,
∴O,S,N,L四点共圆,
同理:O,T,M,S四点共圆,
∴∠STM=∠SOM,∠SLN=∠SON,
∴∠SON=∠SOM,
∵OS⊥AB,
∴MS=NS,
∴CM•MF=AM•MB,EN•ND=BN•NA,
∵AM=BN,BM=AN,
∴CM•MF=EN•ND.
点评 此题是圆的综合题,主要考查了相似三角形的判定和性质,圆的性质,垂径定理,勾股定理,四点共圆,四边形的面积的求法,相交弦定理,解本题的关键是用勾股定理和垂径定理,作出辅助线是解本题的难点,是一道比较麻烦的试题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1≤y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
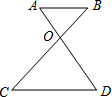 如图AB∥CD,AD、BC交于O点,则下列各式:
如图AB∥CD,AD、BC交于O点,则下列各式:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com