
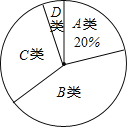
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),按测试成绩m(单位:分)分为A、B、C、D四个组别并绘制出以下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)在被调查的男生中,成绩等级为D的男生有 人,成绩等级为A的男生人数占被调查男生人数的百分比为 %;
(2)本次抽取样本容量为 ,成绩等级为C的男生有 人;
(3)若该校九年级男生有300名,估计成绩少于9分的男生人数.
分组 | 成绩 | 人数 |
A | 12≤m≤15 | 10 |
B | 9≤m≤11 | 22 |
C | 6≤m≤8 | |
D | m≤5 | 3 |
【答案】(1)3,20;(2)50,15;(3)估计成绩少于9分的男生人数有108人
【解析】
(1)根据表格中的数据可以得到成绩等级为D的男生和成绩等级为A的男生人数占被调查男生人数的百分比;
(2)根据表格中的数据可以得到本次抽取样本容量和成绩等级为C的男生人数;
(3)根据表格中的数据可以算出该校九年级成绩少于9分的男生人数.
解:(1)由表格可知,
成绩等级为D的男生有3人,
调查的人数为:10÷20%=50(人),
成绩等级为A的男生人数占被调查男生人数的百分比为:10÷50×100%=20%,
故答案为:3,20;
(2)调查的人数为:10÷20%=50(人),
成绩等级为C的男生有:50﹣10﹣22﹣3=15(人),
故答案为:50,15;
(3)300×![]() =108(人)
=108(人)
答:估计成绩少于的男生人数有108人.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家购A、B两种品牌店化妆品,若购进![]() 品牌的化妆品5套,
品牌的化妆品5套,![]() 品牌的化妆品6套,需要950元;若购进
品牌的化妆品6套,需要950元;若购进![]() 品牌的化妆品3套,
品牌的化妆品3套,![]() 品牌的化妆品2套,需要450元.
品牌的化妆品2套,需要450元.
(1)求![]() 、
、![]() 两种品牌的化妆品每套进价分别为多少元?
两种品牌的化妆品每套进价分别为多少元?
(2)若销售1套![]() 品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进
品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进![]() 品牌化妆品的数量比购进
品牌化妆品的数量比购进![]() 品牌的化妆品数量的2倍还多4套,且
品牌的化妆品数量的2倍还多4套,且![]() 品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, ![]() .
.

(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当![]() 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠B=30°,点D在BA的延长线上,点E在BC边上,连接DE,交AC于点F.若∠EFC=60°,DE=2AC,求![]() 的值.某学习小组的同学经过思考,交流了自己的想法:
的值.某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现∠C与∠D存在某种数量关系”;
小强:“通过构造三角形,证明三角形相似,进而可以求得![]() 的值.
的值.
老师:如图2,将原题中“点D在BA的延长线上,点E在BC边上”改为“点D在AB边上,点E在BC的延长线上”,添加条件“BC=5![]() ,EC=4
,EC=4![]() ”,其它条件不变,可求出△BED的面积.
”,其它条件不变,可求出△BED的面积.
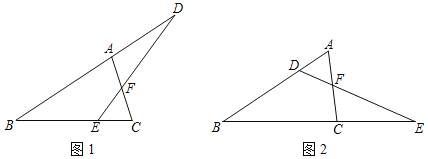
请回答:
(1)用等式表示∠C、∠D的数量关系并证明;
(2)求![]() 的值;
的值;
(3)△BDE的面积为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
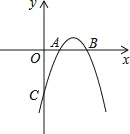
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)将该抛物线向左平移 个单位长度后,可使平移后的抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式: ;
(3)观察图象,写出关于x的不等式ax2+bx+c+3>0的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
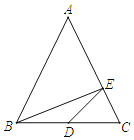
【题目】如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=![]() x2+
x2+![]() B.y=
B.y=![]() x2+
x2+![]()
C.y=![]() x2+2D.y=
x2+2D.y=![]() x2+2
x2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
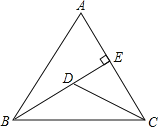
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+![]() BD的最小值是( )
BD的最小值是( )
A.2![]() B.4
B.4![]() C.5
C.5![]() D.10
D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com