练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    边长为2的等边三角形ABC内接于⊙O，则圆心O到△ABC一边的距离为    ．
    【答案】分析：连接中心与一边的端点，作出弦心距，就可以得到直角三角形，解直角三角形即可求解．
    解答：解：连接OA，并作OD⊥AB于D，
    ∵△ABC是等边三角形，
    ∴∠OAD=∠A=30°，OA=1；
    ∴OD=OA tan30°=．
    点评：本题考查了三角形的内切圆与内心的计算．解这类题一般都利用过内心向正三角形的一边作垂线，则正三角形的半径、内切圆半径和正三角形边长的一半构成一个直角三角形，解这个直角三角形，可求出相关边长或角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知：如图，边长为2
    		3
    的等边三角形ABC内接于⊙O，点D在
    AC
    上运动，但与A、C两点不精英家教网重合，连接AD并延长交BC的延长结于P．
    （1）求⊙O的半径；
    （2）设AD为x，AP为y，写出y与x的函数关系式及自变量x的取值范围；
    （3）D点在运动过程中是否存在这样的位置，使得△BDP成为以DB、DP为腰的等腰三角形？若存在，请你求出此时AD的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    27、阅读：我们把边长为1的等边三角形PQR沿着边长为整数的正n（n＞3）边形的边按照如图1的方式连续转动，当顶点P回到正n边形的内部时，我们把这种状态称为它的“点回归”；当△PQR回到原来的位置时，我们把这种状态称为它的“三角形回归”．
    例如：如图2，

    边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内，顶点Q与点A重合，顶点R与点B重合，△PQR沿着正方形ABCD的边BC、CD、DA、AB…连续转动，当△PQR连续转动3次时，顶点P回到正方形ABCD内部，第一次出现P的“点回归”；当△PQR连续转动4次时△PQR回到原来的位置，出现第一次△PQR的“三角形回归”．
    操作：如图3，

    如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动，则连续转动的次数
    k=
    3
    时，第一次出现P的“点回归”；连续转动的次数k=
    5
    时，第一次出现△PQR的“三角形回归”．
    猜想：
    我们把边长为1的等边三角形PQR沿着边长为1的正n（n＞3）边形的边连续转动，
    （1）连续转动的次数k=
    3
    时，第一次出现P的“点回归”；
    （2）连续转动的次数k=
    n
    时，第一次出现△PQR的“三角形回归”；
    （3）第一次同时出现P的“点回归”与△PQR的“三角形回归”时，写出连续转动的次数k与正多边形的边数n之间的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•普陀区一模）把两块边长为4的等边三角板ABC和DEF先如图1放置，使三角板DEF的顶点D与三角板ABC的AC边的中点重合，DF经过点B，射线DE与射线AB相交于点M，接着把三角形板ABC固定不动，将三角形板DEF由图11-1所示的位置绕点D按逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，射线DF与线段BC相交于点N（如图2示）．
    （1）当0°＜α＜60°时，求AM•CN的值；
    （2）当0°＜α＜60°时，设AM=x，两块三角形板重叠部分的面积为y，求y与x的函数解析式并求定义域；
    （3）当BM=2时，求两块三角形板重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源：第1章《反比例函数》中考题集（25）：1.3 实际生活中的反比例函数（解析版） 题型：解答题

    如图所示，边长为2的等边三角形OAB的顶点A在x轴的正半轴上，B点位于第一象限，将△OAB绕O点顺时针旋转30°后，恰好A点在双曲线y=（x＞0）上．
    （1）求双曲线y=（x＞0）的解析式；
    （2）等边三角形OAB继续按顺时针方向旋转多少度后，A点再次落在双曲线上？

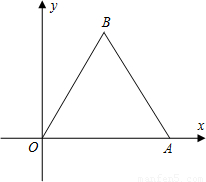
    查看答案和解析>>

    科目：初中数学 来源：江苏期末题 题型：解答题

    阅读：我们把边长为1的等边三角形PQR沿着边长为整数的正n（n＞3）边形的边按照如图1的方式连续转动，当顶点P回到正n边形的内部时，我们把这种状态称为它的“点回归”；当△PQR回到原来的位置时，我们把这种状态称为它的“三角形回归”。
    例如：如图2，边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内，顶点Q与点A重合，顶点R与点B重合，△PQR沿着正方形ABCD的边BC、CD、DA、AB……连续转动，当△PQR连续转动3次时，顶点P回到正方形ABCD内部，第一次出现P的“点回归”；当△PQR连续转动4次时△PQR回到原来的位置，出现第一次△PQR的“三角形回归”。
    操作：如图3，如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动，则连续转动的次数k=（    ）时，第一次出现P的“点回归”；连续转动的次数k=（    ）时，第一次出现△PQR的“三角形回归”。
    猜想：我们把边长为1的等边三角形PQR沿着边长为1的正n（n＞3）边形的边连续转动，
    （1）连续转动的次数k=（    ）时，第一次出现P的“点回归”；
    （2）连续转动的次数k=（    ）时，第一次出现△PQR的“三角形回归”；
    （3）第一次同时出现P的“点回归”与△PQR的“三角形回归”时，写出连续转动的次数k与正多边形的边数n之间的关系。

    查看答案和解析>>

    同步练习册答案