练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
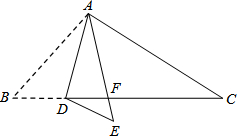
    11．如图，在△ABC中，点D是BC边上的一点，∠B=50°，∠BAD=30°，将△ABD沿AD折叠得到△AED，AE与BC交于点F．则∠EDF的度数是20°．

    分析 先根据折叠性质得：∠BAD=∠EAD=30°，∠E=∠B=50°，再根据外角定理求∠AFC=110°，由三角形内角和可以得出∠EDF为20°．

    解答 解：由折叠得：∠BAD=∠EAD=30°，∠E=∠B=50°，
    ∵∠B=50°，
    ∴∠AFC=∠B+∠BAE=50°+60°=110°，
    ∴∠DFE=∠AFC=110°，
    ∴∠EDF=180°-∠E-∠DFE=180°-50°-110°=20°，
    故答案为：20°．

    点评 本题是折叠问题，考查了折叠的性质和外角定理：①折叠前后的两个角对应相等；②三角形的一个外角等于与它不相邻的两个内角的和；与对顶角性质和三角形内角和定理求出角的度数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．如图，在四边形ABCD中，∠ACB=∠ADB=90°，E、F分别是AB、AD的中点，则EF与CD有什么关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图所示，作字母“E”关于y轴对称的图形，并写出所得图形相应各点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图所示，在一次“寻宝”游戏中，已知寻宝图上两个标志点A（-3，0）和点B（5，0），宝藏分别埋在C（3，4）和D（-2，3）两点．请你首先建立直角坐标系确定宝藏的位置，然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图所示，在△ABC中，∠B=70°，∠C=60°，直线DE交AC于点D，交AB于点E，如果∠1=95°，则∠2=145°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．两根木棒的长分别是7cm和9cm，现要你选择第3根木棒，将它们钉成一个三角形，若选择的木棒长度是7的倍数，则你选择的木棒的长为14cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在矩形ABCD中，对角线BD与边BC所构成的锐角∠DBC=30°，已知DC=2cm，则该矩形的面积是4$\sqrt{3}$cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．在△ABC中，已知a=2$\sqrt{2}$，b=$\sqrt{3}$，∠C=60°，则△ABC的面积为$\frac{3\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

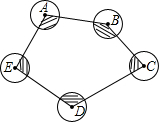    1．如图，五个半径为2的圆，圆心分别是点A，B，C，D，E，则图中阴影部分的面积和是多少？（S扇形=$\frac{nπR^2}{360°}$）

    查看答案和解析>>

    同步练习册答案