(1)证明:∵AB是直径,CD是弦,CD⊥AB,
∴

=

.
∴∠ADC=∠AFD.
又∵四边形AFCD内接于⊙O,∠FCM=∠FAD,∠CFM=∠ADC,
∴∠AFD=∠CFM.
∴△AFD∽△CFM;
(2)存在,当点F运动到弧AC的中点时,△FMD为等腰三角形.
证明:当点F在AC中点时,∠ADF=∠CDF,
又由(1)△AFD∽△CFM,
∴∠M=∠ADF.
∴∠M=∠CDF.
∴FD=FM,即△FMD为等腰三角形.
分析:(1)证△AFD∽△CFM,需找出两组对应角相等;根据圆内接四边形的性质,易求得∠MCF=∠FAD,∠MFC=∠MDA.因此还需找出一组对应角相等.已知直径AB⊥CD,根据垂径定理知:弧AC=弧AD,可得∠MDA=∠MFC,即∠MFC=∠AFD,由此得证;
(2)由(1)知∠M=∠ADF,要使△FMD为等腰三角形,则必须有∠M=∠FDC,因此只要∠FDC=∠ADF即可,这就要求F必须运动到弧AC的中点.
点评:解此题的关键是把点的运动抽象到相似三角形中来考虑,培养同学的推理能力,难易程度适中.

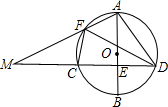 AC上从A点向C点运动(点A、C除外),AF与DC的延长线相交于点M.
AC上从A点向C点运动(点A、C除外),AF与DC的延长线相交于点M. =
= .
.

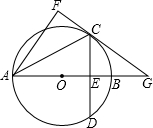 C与直线AB相交于点G.
C与直线AB相交于点G.