如图.从点A(0.2)发出一束光.经x轴反射.过点B(4.3).则这束光从点A到点B所经过的路径的长为． [解析][解析] 如图.延长BC.交y轴于点D.过点B作BE∥y轴.过点D作DE∥x轴．∵从点A(0.2)发出的一束光.经x轴反射.过点B(4.3).∴AC=CD.OA=OD=2.∵点B(4.3).∴DE=4.BE=3+2=5.∴BD==.∴这束光从点A到点B所经过题目和参考答案——青夏教育精英家教网—

如图，从点A（0，2）发出一束光，经x轴反射，过点B（4，3），则这束光从点A到点B所经过的路径的长为_____．

【解析】【解析】如图，延长BC，交y轴于点D，过点B作BE∥y轴，过点D作DE∥x轴．∵从点A（0，2）发出的一束光，经x轴反射，过点B（4，3），∴AC=CD，OA=OD=2，∵点B（4，3），∴DE=4，BE=3+2=5，∴BD==，∴这束光从点A到点B所经过路径的长为．故答案为：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2017-2018学年九年级数学北师大版上册第3章概率的进一步认识单元测试卷 题型：填空题

在m2□6m□9的“□”中任意填上“+”或“﹣”号，所得的代数式为完全平方式的概率为___________．

．【解析】试题分析：先画树状图展示所有四种等可能的结果数，再根据完全平方式的定义得到“++”和“﹣+”能使所得的代数式为完全平方式，然后根据概率公式求解．画树状图为：共有四种等可能的结果数，其中“++”和“﹣+”能使所得的代数式为完全平方式，所以所得的代数式为完全平方式的概率==．

查看答案和解析>>

科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：解答题

（8分）解不等式组 ;

【解析】试题分析：先解不等式①求得解集是；再解不等式②求得解集是；然后求出两个解集的公共部分即可. ，解①得，；解②得，； ∴不等式组的解集是.

查看答案和解析>>

科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：单选题

估计的值（）

A. 在1和2之间 B. 在2和3之间 C. 在3和4之间 D. 在4和5之间

C 【解析】∵， ∴，故选C.

查看答案和解析>>

科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：解答题

如图，将竖直放置的长方形砖块ABCD推倒至长方形A'B'C'D'的位置，长方形ABCD的长和宽分别为a，b，AC的长为c.

（1）你能用只含a，b的代数式表示S△ABC，S△C'A'D'和S直角梯形A'D'BA吗?能用只含c的代数式表示S△ACA'吗?

（2）利用(1)的结论，你能验证勾股定理吗?

（1）S△ABC=ab，S△C'A'D'=ab，S直角梯形A'D'BA= (a+b)(a+b)= (a+b)2，S△ACA'=c2；（2）验证见解析. 【解析】试题分析：（1）易知△ABC，△C'A'D'和△ACA'都是直角三角形，根据三角形面积公式和梯形面积公式计算即可；（2）根据S△ACA'=S直角梯形A'D'BA-S△ABC-S△C'A'D，列出方程并整理即可得到结论．...

查看答案和解析>>

科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：单选题

如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线上D'处.若AB=3，AD=4，则ED的长为(　　)

A. B. 3 C. 1 D.

A 【解析】首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△D′EC，设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，再根据勾股定理可得方程22+x2=（4﹣x）2，再解方程即可．【解析】 ∵AB=3，AD=4， ∴DC=3， ∴AC==5，根据折叠可得：△DEC≌△D′EC， ∴D′C=DC=3，DE=D′E，设ED=...

查看答案和解析>>

科目：初中数学 来源：2018人教版八年级数学下册练习：第十七章达标检测卷 题型：单选题

如图，已知正方形B的面积为144，正方形C的面积为169时，那么正方形A的面积为（）

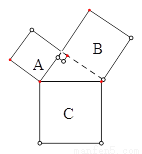
A. 313 B. 144 C. 169 D. 25

D 【解析】设三个正方形的边长依次为，由于三个正方形的三边组成一个直角三角形，所以，故，即.

查看答案和解析>>

科目：初中数学 来源：湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型：填空题

已知tanA=，则锐角A的度数是__________．

30° 【解析】根据特殊角的三角函数值，可知∠A=30°. 故答案为：30°.

查看答案和解析>>

科目：初中数学 来源：山西省吕梁市孝义市2016-2017学年九年级（上）期末考试数学试卷 题型：解答题

解下列方程

（1）2x2﹣4x=12

（2）4x（2x+1）=6x+3．

(1)x=1±（2）x=﹣或x= 【解析】试题分析：（1）用配方法求【解析】方程两边除以2把二次项系数化为1，然后两边加上一次项系数一半的平方，使左边化为完全平方式，右边是常数项，然后直接开平方求解即可；（2）把方程右边的项提出公因式3后移至左边，再利用提出公因式(2x＋1)，使方程转化为两个因式的积等于0的形式，然后转化为两个一元一次方程求解即可．试题解析：【解...

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学