
 ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßC0£ŗy=x2£¬¶„µć¼Ē×÷A0£®Ź×ĻČĪŅĆĒ½«Å×ĪļĻßC0¹ŲÓŚÖ±Ļßy=1¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßC1³ĘĪŖµŚŅ»“Ī²Ł×÷£¬ŌŁ½«Å×ĪļĻßC1¹ŲÓŚÖ±Ļßy=2¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßC2³ĘĪŖµŚ¶ž“Ī²Ł×÷£¬”£¬½«Å×ĪļĻßCn-1¹ŲÓŚÖ±Ļßy=2n-1¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßCn£Ø¶„µć¼Ē×÷An£©³ĘĪŖµŚn“Ė²Ł×÷£Øn=1£¬2£¬3”£©£¬”£®ÉčÅ×ĪļĻßC0ÓėÅ×ĪļĻßC1½»ÓŚĮ½µćB0ÓėB1£¬Ė³“ĪĮ¬½ÓA0”¢B0”¢A1”¢B1ĖÄøöµćµĆµ½ĖıߊĪA0B0A1B1£¬Å×ĪļĻßC2ÓėÅ×ĪļĻßC3½»ÓŚĮ½µćB2ÓėB3£¬Ė³“ĪĮ¬½ÓA2”¢B2”¢A3”¢B3ĖÄøöµćµĆµ½ĖıߊĪA2B2A3B3£¬”£¬Å×ĪļĻßCk-1ÓėÅ×ĪļĻßCk½»ÓŚĮ½µćBk-1ÓėBk£¬Ė³“ĪĮ¬½ÓAk-1”¢Bk-1”¢Ak”¢BkĖÄøöµćµĆµ½ĖıߊĪAk-1Bk-1AkBk£Øk=1£¬3£¬5”£©£¬”£®
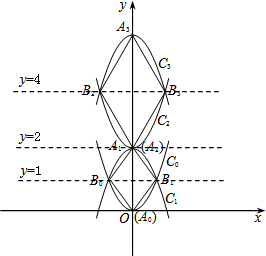
ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßC0£ŗy=x2£¬¶„µć¼Ē×÷A0£®Ź×ĻČĪŅĆĒ½«Å×ĪļĻßC0¹ŲÓŚÖ±Ļßy=1¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßC1³ĘĪŖµŚŅ»“Ī²Ł×÷£¬ŌŁ½«Å×ĪļĻßC1¹ŲÓŚÖ±Ļßy=2¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßC2³ĘĪŖµŚ¶ž“Ī²Ł×÷£¬”£¬½«Å×ĪļĻßCn-1¹ŲÓŚÖ±Ļßy=2n-1¶Ō³Ę·ÕŪ¹żČ„µĆµ½Å×ĪļĻßCn£Ø¶„µć¼Ē×÷An£©³ĘĪŖµŚn“Ė²Ł×÷£Øn=1£¬2£¬3”£©£¬”£®ÉčÅ×ĪļĻßC0ÓėÅ×ĪļĻßC1½»ÓŚĮ½µćB0ÓėB1£¬Ė³“ĪĮ¬½ÓA0”¢B0”¢A1”¢B1ĖÄøöµćµĆµ½ĖıߊĪA0B0A1B1£¬Å×ĪļĻßC2ÓėÅ×ĪļĻßC3½»ÓŚĮ½µćB2ÓėB3£¬Ė³“ĪĮ¬½ÓA2”¢B2”¢A3”¢B3ĖÄøöµćµĆµ½ĖıߊĪA2B2A3B3£¬”£¬Å×ĪļĻßCk-1ÓėÅ×ĪļĻßCk½»ÓŚĮ½µćBk-1ÓėBk£¬Ė³“ĪĮ¬½ÓAk-1”¢Bk-1”¢Ak”¢BkĖÄøöµćµĆµ½ĖıߊĪAk-1Bk-1AkBk£Øk=1£¬3£¬5”£©£¬”£®·ÖĪö £Ø1£©øł¾ŻÅ×ĪļĻߵĶ„µćµÄ±ä»Æ¹ęĀÉŠ“³ö½āĪöŹ½¼“æÉ£»
£Ø2£©ĻČøł¾Ż¶Ō½ĒĻß»„Ļą“¹Ö±Ę½·ÖµĆ³öĖıߊĪ¶¼ŹĒĮāŠĪ£¬ŌŁĖµĆ÷ĖıߊĪA0B0A1B1ŗĶĖıߊĪA2B2A3B3²»ĻąĖĘ£¬ĄķÓÉŹĒ£ŗĖıߊĪA0B0A1B1ĪŖÕż·½ŠĪ£¬ĖıߊĪA2B2A3B3ĪŖĮāŠĪ£»
£Ø3£©øł¾ŻÅ×ĪļĻßCnµÄ½āĪöŹ½ŹĒÅ×ĪļĻßCk-1¹ŲÓŚÖ±Ļßy=2k-1·ÕŪµĆµ½Å×ĪļĻßCkĖłĪ§³ÉµÄĶ¼ŠĪŹĒĖıߊĪAk-1Bk-1AkBk£ØĮāŠĪ£©£¬ŌŁÓÉĮāŠĪµÄĆ껿¹«Ź½æÉµĆ³öĘäĆ껿£®
½ā“š ½ā£ŗ£Ø1£©C1£ŗy=-x2+2£»C2£ŗy=x2+2£»C3£ŗy=-x2+6£»C4£ŗy=x2+10£®
£Ø2£©øł¾ŻÅ×ĪļĻߵĶŌ³ĘŠŌŅŌ¼°·ÕŪµÄŌĄķ²»ÄŃµĆ³öĖıߊĪAk-1Bk-1AkBk£Øk=1£¬3£¬5”£©µÄĮ½Ģõ¶Ō½ĒĻßBk-1BkÓėAk-1Ak»„Ļą“¹Ö±ĒŅĘ½·Ö£¬¹ŹŅ»ĻµĮŠĖıߊĪAk-1Bk-1AkBk¾łĪŖĮāŠĪ£»ĖüĆĒ²¢²»¶¼ĻąĖĘ£¬·“Ąż£ŗĖıߊĪA0B0A1B1ŗĶĖıߊĪA2B2A3B3²»ĻąĖĘ£¬
ĄķÓÉČēĻĀ£ŗ
²»ÄŃĖć³öA0A1=B0B1=2£¬ÓŚŹĒĖıߊĪA0B0A1B1ĪŖÕż·½ŠĪ£®
¶ųA2A3=4£¬${B_2}{B_3}=2\sqrt{2}$£¬
”ąA2A3”ŁB2B3£¬
”ąĖıߊĪA2B2A3B3ĪŖĮāŠĪ£¬
”ąĖüĆĒ²»ĻąĖĘ£®
£Ø3£©Å×ĪļĻßCnµÄ½āĪöŹ½ĪŖ£ŗ$\left\{\begin{array}{l}y={x^2}+\frac{{{2^{n+1}}-2}}{3}£Ønż£©\\ y=-{x^2}+\frac{{{2^{n+1}}+2}}{3}£ØnĘę£©\end{array}\right.$£¬£Ø»ņ$y={£Ø-1£©^n}•{x^2}+\frac{{{2^{n+1}}+{{£Ø-1£©}^{n+1}}•2}}{3}$£®£©
ÓÉÓŚĖıߊĪAk-1Bk-1AkBk £Øk=1£¬3£¬5”£©ŹĒÅ×ĪļĻßCk-1¹ŲÓŚÖ±Ļßy=2k-1·ÕŪµĆµ½Å×ĪļĻßCkĖłĪ§³ÉµÄĶ¼ŠĪ£¬ĄūÓĆÉĻŹö½įĀŪ²»ÄŃµĆ³ö£ŗ${A}_{k-1}{A}_{k}=\frac{{2}^{k+1}+2}{3}-\frac{{2}^{k}-2}{3}=\frac{{2}^{k}+4}{3}$£¬
”ą$\left\{\begin{array}{l}{{C}_{k-1}£ŗy={x}^{2}+\frac{{2}^{k}-2}{3}}\\{{C}_{k}£ŗy=-{x}^{2}+\frac{{2}^{k+1}+2}{3}}\end{array}\right.$£®
”ą$\left\{\begin{array}{l}{{x}_{{B}_{k-1}}=-\sqrt{\frac{{2}^{k-1}+2}{3}}}\\{{x}_{{B}_{k}}=\sqrt{\frac{{2}^{k-1}+2}{3}}}\end{array}\right.$£®
”ą${B}_{k-1}{B}_{k}={x}_{{B}_{k}}-{x}_{{B}_{k-1}}=2\sqrt{\frac{{2}^{k-1}+2}{3}}$£®£Ø»ņÕßĒó½ā$\left\{\begin{array}{l}y={2^{k-1}}\\ y={x^2}+\frac{{{2^{n+1}}-2}}{3}£Ønż£©\end{array}\right.$£©£®
”ą${{S}_{{A}_{k-1}{B}_{k-1}{A}_{k}B}}_{k}=\frac{1}{2}•{A}_{k-1}{A}_{k}•{B}_{k-1}{B}_{k}$=$\frac{{2}^{k}+4}{3}•\sqrt{\frac{{2}^{k-1}+2}{3}}$=$\frac{{2\sqrt{3}}}{9}•£Ø{2^{k-1}}+2£©•\sqrt{{2^{k-1}}+2}$£®
µćĘĄ ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹżµÄÖį¶Ō³Ę±ä»»”¢Ę½ŠŠĖıߊĪµÄÅŠ¶ØŗĶŠŌÖŹŅŌ¼°ĮāŠĪ”¢Õż·½ŠĪµÄÅŠ¶ØŗĶŠŌÖŹ£¬ÓƵ½µÄÖŖŹ¶µć»¹ÓŠŅ»ŌŖ¶ž“Ī·½³ĢµÄ½ā·ØŅŌ¼°·ÖĄąĢÖĀŪµÄŹżŃ§Ė¼Ļė£¬ĢāÄæµÄ×ŪŗĻŠŌŗÜĒæ°üŗ¬ÄŚČŻ½Ļ¶ą£¬ÄѶČŗÜ“ó£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | x£¾1 | B£® | x£¾0 | C£® | x”Ł0 | D£® | x”Ł1 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
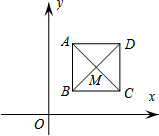 ČēĶ¼£¬ŅŃÖŖÕż·½ŠĪABCD£¬¶„µćA£Ø1£¬3£©£¬B£Ø1£¬1£©£¬C£Ø3£¬1£©£¬¶Ō½ĒĻß½»ÓŚµćM£®¹ę¶Ø”°°ŃÕż·½ŠĪABCDĻČŃŲxÖį·ÕŪ£¬ŌŁĻņ×óĘ½ŅĘøöµ„Ī»”±ĪŖŅ»“Ī±ä»»£¬ÄĒĆ“¾¹żĮ½“Ī±ä»»ŗ󣬵ćMµÄ×ų±ź±äĪŖ£Ø0£¬2£©£¬Į¬Šų¾¹ż2015“Ī±ä»»ŗ󣬵ćMµÄ×ų±ź±äĪŖ£Ø-2013£¬-2£©£®
ČēĶ¼£¬ŅŃÖŖÕż·½ŠĪABCD£¬¶„µćA£Ø1£¬3£©£¬B£Ø1£¬1£©£¬C£Ø3£¬1£©£¬¶Ō½ĒĻß½»ÓŚµćM£®¹ę¶Ø”°°ŃÕż·½ŠĪABCDĻČŃŲxÖį·ÕŪ£¬ŌŁĻņ×óĘ½ŅĘøöµ„Ī»”±ĪŖŅ»“Ī±ä»»£¬ÄĒĆ“¾¹żĮ½“Ī±ä»»ŗ󣬵ćMµÄ×ų±ź±äĪŖ£Ø0£¬2£©£¬Į¬Šų¾¹ż2015“Ī±ä»»ŗ󣬵ćMµÄ×ų±ź±äĪŖ£Ø-2013£¬-2£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
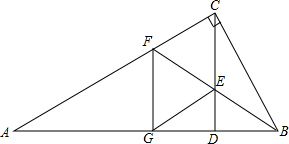 ČēĶ¼£ŗBFŹĒRt”÷ABCµÄ½ĒĘ½·ÖĻߣ¬”ĻACB=90”ć£¬CDŹĒøߣ¬BFÓėCD½»ÓŚµćE£¬EG”ĪAC½»ABÓŚG£®ĒóÖ¤£ŗFG”ĶAB£®
ČēĶ¼£ŗBFŹĒRt”÷ABCµÄ½ĒĘ½·ÖĻߣ¬”ĻACB=90”ć£¬CDŹĒøߣ¬BFÓėCD½»ÓŚµćE£¬EG”ĪAC½»ABÓŚG£®ĒóÖ¤£ŗFG”ĶAB£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻB”¢”ĻCµÄĘ½·ÖĻß½»ÓŚµćD£®¹żµćD×÷EF”ĪBC£¬ÓėAB½»ÓŚµćE£¬ÓėAC½»ÓŚµćF£®ŅŃÖŖAB=6cm£¬AC=4cm£¬Ēó”÷AEFµÄÖܳ¤£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻB”¢”ĻCµÄĘ½·ÖĻß½»ÓŚµćD£®¹żµćD×÷EF”ĪBC£¬ÓėAB½»ÓŚµćE£¬ÓėAC½»ÓŚµćF£®ŅŃÖŖAB=6cm£¬AC=4cm£¬Ēó”÷AEFµÄÖܳ¤£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
 ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDÖŠ£¬µćEŹĒ±ßADµÄŅ»øöČżµČ·Öµć£¬EC½»¶Ō½ĒĻßBDÓŚµćF£¬ŌņFC£ŗECµČÓŚ£Ø””””£©
ČēĶ¼£¬Ę½ŠŠĖıߊĪABCDÖŠ£¬µćEŹĒ±ßADµÄŅ»øöČżµČ·Öµć£¬EC½»¶Ō½ĒĻßBDÓŚµćF£¬ŌņFC£ŗECµČÓŚ£Ø””””£©| A£® | 3£ŗ2 | B£® | 3£ŗ4 | C£® | 1£ŗ1 | D£® | 1£ŗ2 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com